The elastic buckling of long thin cylinders is a classic problem
in structural mechanics. It has long been recognized experimentally that
the buckle pattern occurs locally along the axial length of the cylinder.
However the standard classic approach assumes that the buckle pattern comprises
of an interaction of periodic eigenmodes axially and circumferentially.
In our work we treat the buckling as a localization phenomenon.
The most widely used model for the buckling of thin cylinders rests with the von Karman-Donnell equations:
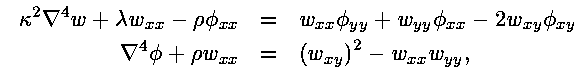
governing radial displacement w and in-plane stress ![]() .
.
The parameters appearing are the curvature rho := 1/R,![]() where nu is Poisson's ratio and the bifurcation parameter
where nu is Poisson's ratio and the bifurcation parameter![]() where P is the compressive axial load applied per unit length and E is
Young's modulus. The equations are supplemented with periodic boundary
conditions in the circumferential direction and asymptotic boundary conditions
in the axial direction.
where P is the compressive axial load applied per unit length and E is
Young's modulus. The equations are supplemented with periodic boundary
conditions in the circumferential direction and asymptotic boundary conditions
in the axial direction.
We discretize in the circumferential direction by a Galerkin method
to get a nasty looking system of ODEs.
Here are the first 6 Fourier modes for
the displacement and stress. We clearly see the localized nature of the
solution. The modes are shown at a minimum load. This was found by numerical
continuation using the code auto.
A typical bifurcation diagram looks like this![]()
Here we have reconstructed the solution over the cylinder for the displacement
w (on left) and the stress![]() (on
the right or below)
(on
the right or below)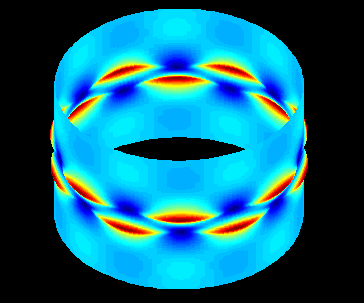
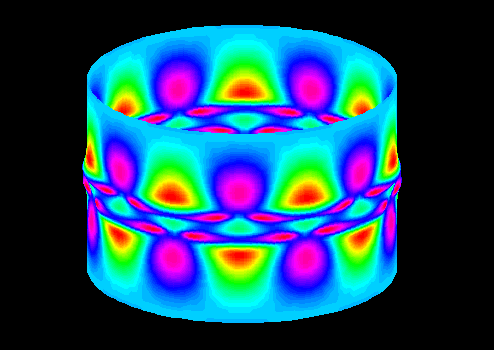
![]() A large AVI Movie
A large AVI Movie


 This page was written and maintained by Gabriel Lord
This page was written and maintained by Gabriel Lord