Figure 1.
This is a local copy of the HTML version of Reynold's Classic paper on flocking: It comes from here:
http://www.cs.toronto.edu/~dt/siggraph97-course/cwr87/
Craig W. Reynolds
Symbolics Graphics Division
[obsolete addresses removed 2]
The aggregate motion of a flock of birds, a herd of land animals, or a school of fish is a beautiful and familiar part of the natural world. But this type of complex motion is rarely seen in computer animation. This paper explores an approach based on simulation as an alternative to scripting the paths of each bird individually. The simulated flock is an elaboration of a particle system, with the simulated birds being the particles. The aggregate motion of the simulated flock is created by a distributed behavioral model much like that at work in a natural flock; the birds choose their own course. Each simulated bird is implemented as an independent actor that navigates according to its local perception of the dynamic environment, the laws of simulated physics that rule its motion, and a set of behaviors programmed into it by the "animator." The aggregate motion of the simulated flock is the result of the dense interaction of the relatively simple behaviors of the individual simulated birds.
Categories and Subject Descriptors: 1.2.10 [Artificial Intelligence]: Vision and Scene Understanding; 1.3.5 [Computer Graphics]: Computational Geometry and Object Modeling; 1.3.7 [Computer Graphics]: Three Dimensional Graphics and Realism-Animation: 1.6.3 [Simulation and Modeling]: Applications.
General Terms: Algorithms, design.b
Additional Key Words, and Phrases: flock, herd, school, bird, fish, aggregate motion, particle system, actor, flight, behavioral animation, constraints, path planning.
The motion of a flock of birds is one of nature's delights. Flocks and related synchronized group behaviors such as schools of fish or herds of land animals are both beautiful to watch and intriguing to contemplate. A flock* exhibits many contrasts. It is made up of discrete birds yet overall motion seems fluid; it is simple in concept yet is so visually complex, it seems randomly arrayed and yet is magnificently synchronized. Perhaps most puzzling is the strong impression of intentional, centralized control. Yet all evidence indicates that flock motion must be merely the aggregate result of the actions of individual animals, each acting solely on the basis of its own local perception of the world.
One area of interest within computer animation is the description and control of all types of motion. Computer animators seek both to invent wholly new types of abstract motion and to duplicate (or make variations on) the motions found in the real world. At first glance, producing an animated, computer graphic portrayal of a flock of birds presents significant difficulties. Scripting the path of a large number of individual objects using traditional computer animation techniques would be tedious. Given the complex paths that birds follow, it is doubtful this specification could be made without error. Even if a reasonable number of suitable paths could be described, it is unlikely that the constraints of flock motion could be maintained (for example, preventing collisions between all birds at each frame). Finally, a flock scripted in this manner would be hard to edit (for example, to alter the course of all birds for a portion of the animation). It is not impossible to script flock motion, but a better approach is needed for efficient, robust, and believable animation of flocks and related group motions.
This paper describes one such approach. This approach assumes a flock is simply the result of the interaction between the behaviors of individual birds. To simulate a flock we simulate the behavior of an individual bird (or at least that portion of the bird's behavior that allows it to participate in a flock). To support this behavioral "control structure," we must also simulate portions of the bird's perceptual mechanisms and aspects of the physics of aerodynamic flight. If this simulated bird model has the correct flock-member behavior, all that should be required to create a simulated flock is to create some instances of the simulated bird model and allow them to interact.**
Some experiments with this sort of simulated flock are described in more detail in the remainder of this paper. The success and validity of these simulations is difficult to measure objectively. They do seem to agree well with certain criteria [25] and some statistical properties [23] of natural flocks and schools which have been reported by the zoological and behavioral sciences. Perhaps more significantly, many people who view these animated flocks immediately recognize them as a representation of a natural flock, and find them similarly delightful to watch.
The computer graphics community has seen simulated bird flocks before. The Electronic Theater at SIGGRAPH `85 presented a piece labeled "motion studies for a work in progress entitled `Eurythmy'" [4] by Susan Amkraut, Michael Girard, and George Karl from the Computer Graphics Research Group of Ohio State University. In the film, a flock of birds flies up out of a minaret and, passing between a series of columns, flies down into a lazy spiral around a courtyard. All the while the birds slowly flap their wings and avoid collision with their flockmates.
That animation was produced using a technique completely unlike the one described in this paper and apparently not specifically intended for flock modeling. But the underlying concept is useful and interesting in its own right. The following overview is based on unpublished communications [3]. The software is informally called "the force field animation system." Force fields are defined by a 3 x 3 matrix operator that transform from a point in space (where an object is located) to an acceleration vector: the birds trace paths along the "phase portrait" of the force field. There are "rejection forces" around each bird and around static objects. The force field associated with each object has a bounding box, so object interactions can be culled according to bounding box tests. An incremental, linear time algorithm finds bounding box intersections. The "animator" defines the space field(s) and sets the initial positions, orientations, and velocities of objects. The rest of the simulation is automatic.
Karl Sims of MIT's Media Lab has constructed some behaviorally controlled animation of groups of moving objects (spaceships, inchworms, and quadrupeds), but they are not organized as flocks [35]. Another author kept suggesting [28, 29, 30] implementing a flock simulation based on a distributed behavioral model.
The simulated flock described here is closely related to particle systems [27], which are used to represent dynamic "fuzzy objects" having irregular and complex shapes. Particle systems have been used to model fire, smoke, clouds, and more recently, the spray and foam of ocean waves [27]. Particle systems are collections of large numbers of individual particles, each having its own behavior. Particles are created, age, and die off. During their life they have certain behaviors that can alter the particle's own state, which consists of color, opacity, location, and velocity.
Underlying the boid flock model is a slight generalization of particle systems. In what might be called a "subobject system," Reeves's dot-like particles are replaced by an entire geometrical object consisting of a full local coordinate system and a reference to a geometrical shape model. The use of shapes instead of dots is visually significant, but the more fundamental difference is that individual subobjects have a more complex geometrical state; they now have orientation.
Another difference between boid flocks and particle systems is not as well defined. The behavior of boids is generally more complex than the behaviors for particles as described in the literature. The present boid behavior model might be about one or two orders of magnitude more complex than typical particle behavior. However this is a difference of degree, not of kind. And neither simulated behavior is nearly as complex as that of a real bird.
Also, as presented, particles in particle Systems do not interact with one another, although this is not ruled out by definition. But birds and hence boids must interact strongly in order to flock correctly. Boid behavior is dependent not only on internal state but also on external state.
The behavioral model that controls the boid's flight and flocking is complicated enough that rather than use an ad hoc approach, it is worthwhile to pursue the most appropriate formal computational model. The behaviors will be represented as rules or programs in some sense, and the internal state of each boid must be held in some sort of data structure. It is convenient to encapsulate these behaviors and state as an object, in the sense of object-oriented programming systems [10, 11, 21]. Each instance of these objects needs a computational process to apply the behavioral programs to the internal data. The computational abstraction that combines process, procedure, and state is called an actor [12, 26, 2]. An actor is essentially a virtual computer that communicates with other virtual computers by passing messages. The actor model has been proposed as a natural structure for animation control by several authors [28, 13, 29, 18]. It seems particularly apt for situations involving interacting characters and behavior simulation. In the literature of parallel and distributed computer systems, flocks and schools are given as examples of robust self-organizing distributed systems [15].
Traditional hand-drawn cel animation was produced with a medium that was completely inert. Traditional computer animation uses an active medium (computers running graphics software), but most animation systems do not make much use of the computer's ability to automate motion design. Using different tools, contemporary computer animators work at almost the same low level of abstraction as do cel animators. They tell their story by directly describing the motion of their characters. Shortcuts exist in both media: it is common for computer animators and cel animators to use helpers to interpolate between specified keyframes. But little progress has been made in automating motion description; it is up to the animator to translate the nuances of emotion and characterization into the motions that the character performs. The animator cannot simply tell the character to "act happy" but must tediously specify the motion that conveys happiness.
Typical computer animation models only the shape and physical properties of the characters, whereas behavioral or character-based animation seeks to model the behavior of the character. The goal is for such simulated characters to handle many of the details of their actions, and hence their motions. These behaviors include a whole range of activities from simple path planning to complex "emotional" interactions between characters. The construction of behavioral animation characters has attracted many researchers [19, 21, 13, 14, 29, 30, 41, 40], but it is still a young field in which more work is needed.
Because of the detached nature of the control, the person who creates animation with character simulation might not strictly he an animator. Traditionally, the animator is directly responsible for all motion in animation production [40]. It might he more proper to call the person who directs animation via simulated characters a meta-animator, since the animator is less a designer of motion and more a designer of behavior. These behaviors, when acted out by the simulated characters, lead indirectly to the final action. Thus the animator's job becomes somewhat like that of a theatrical director: the character's performance is the indirect result of the director's instructions to the actor. One of the charming aspects of the work reported here is not knowing how a simulation is going to proceed from the specified behaviors and initial conditions; there are many unexpected, pleasant surprises. On the other hand, this charm starts to wear thin as deadlines approach and the unexpected annoyances pop up. This author has spent a lot of time recently trying to get uncooperative flocks to move as intended ("these darn boids seem to have a mind of their own!").
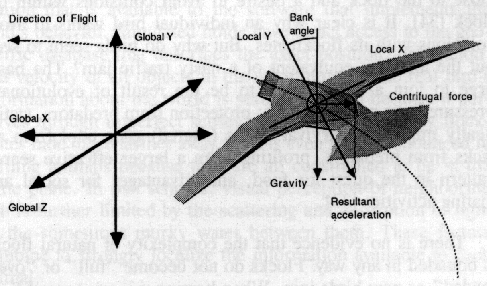
A fundamental part of the boid model is the geometric ability to fly. The motion of the members of a simulated school or herd can be considered a type of "flying" by glossing over the considerable intricacies of wing, fin, and leg motion (and in the case of herds, by restricting freedom of motion in the third dimension). In this paper the term geometric flight refers to a certain type of motion along a path: a dynamic, incremental, rigid geometrical transformation of an object, moving along and tangent to a 3D curve. While the motion is rigid, the object's underlying geometric model is free to articulate or change shape within this "flying coordinate system." Unlike more typical animated motion along predefined spline curves, the shape of a flight path is not specified in advance.
Geometric flight is based on incremental translations along the object's "forward direction," its local positive Z axis. These translations are intermixed with steering-rotations about the local X and Y axes (pitch and yaw), which realign the global orientation of the local Z axis. In real flight, turning and moving happen continuously and simultaneously. Incremental geometric flight is a discrete approximation of this; small linear motions model a continuous curved path. In animation the motion must increment at least once per frame. Running the simulation at a higher rate can reduce the discrete sampling error of the flight model and refine the shape of motion blur patterns.
Flight modeling makes extensive use of the object's own coordinate system. Local space represents the "boid's eye view;" it implies measuring things relative to the boid's own position and orientation. In Cartesian terms, the left/right axis is X, up/down is Y, and forward/pack is Z. The conversion of geometric data between the local and global reference frames is handled by the geometric operators localize and globalize. It is convenient to use a local scale so that the unit of length of the coordinate system is one body length. Biologists routinely specify' flock and school statistics in terms of body lengths.
Geometric flight models conservation of momentum. An object in flight tends to stay in flight. There is a simple model of viscous speed damping, so even if the boid continually accelerates in one direction, it will not exceed a certain maximum speed. A minimum speed can also be specified but defaults to zero. A maximum acceleration, expressed as a fraction of the maximum speed, is used to truncate over-anxious requests for acceleration, hence providing for smooth changes of speed and heading. This is a simple model of a creature with a finite amount of available energy.
Many physical forces are not supported in the current boid model. Gravity is modeled but used only to define banking behavior. It is defined procedurally to allow the construction of arbitrarily shaped fields. If each boid was accelerated by gravity each frame, it would tend to fall unless gravity was countered by lift or buoyancy. Buoyancy is aligned against gravity, but aerodynamic lift is aligned with the boid's local "up" direction and related to velocity. This level of modeling leads to effects like normally level flight, going faster when flying down (or slower up), and the "stall" maneuver. The speed limit parameter could be more realistically modeled as a frictional drag, a backward pointing force related to velocity. In the current model steering is done by directing the available thrust in the appropriate direction. It would be more realistic to separately model the tangential thrusting forces and the lateral steering forces, since they normally have different magnitudes.
Geometric flight relates translation, pitch, and yaw, but does not constrain roil, the rotation about the local Z axis. This degree of freedom is used for banking-rolling the object to align the local Y axis with the (local XY component of the total) acceleration acting upon it. Normally banking is based on the lateral component of the acceleration, but the tangential component can be used for certain applications. The lateral components are from steering and gravity. In straight flight there is no radial force, so the gravitational term dominates and banking aligns the object's -Y axis with "gravitational down" direction. When turning, the radial component grows larger and the "accelerational down" direction swings outward, like a pendulum hanging from the flying object. The magnitude of the turning acceleration varies directly with the object's velocity and with the curvature of its path (so inversely with the radius of its turn). The limiting case of infinite velocity resembles banking behavior in the absence of gravity. In these cases the local + Y (up) direction points directly at the center of curvature defined by the current turn.

Figure 1.
With correct banking (what pilots call a coordinated turn) the object's local space remains aligned with the "perceptual" or "accelerational" coordinate system. This has several advantages: it simplifies the bird's (or pilot's) orientation task, it keeps the lift from the airfoils of the wings pointed in the most efficient direction ("accelerational up"), it keeps the passengers coffee in their cups, and most importantly for animation, it makes the flying boid fit the viewer's expectation of how flying objects should move and orient themselves. On the other hand, realism is not always the goal in animation. By simply reversing the angle of bank we obtain a cartoony motion that looks like the object is being flung outward by the centrifugal force of the turn.
The incremental mixing of forward translations and local rotations that underlies geometric flight is the basis of "turtle graphics" in the programming language Logo [5]. Logo was first used as an educational tool to allow children to learn experimentally about geometry, arithmetic, and programming [22]. The Logo turtle was originally a little mechanical robot that crawled around on large sheets of paper laid on the classroom floor, drawing graphic figures by dragging a felt tip marker along the paper as it moved, Abstract turtle geometry is a system based on the frame of reference of the turtle, an object that unites position and heading. Under program control the Logo turtle could move forward or back from its current position, turn left or right from its current heading, or put the pen up or down on the paper. The turtle geometry has been extended from the plane onto arbitrary manifolds and into 3D space [1]. These "3d turtles" and their paths are exactly equivalent to the boid objects and their flight paths.
"...and the thousands off fishes moved as a huge beast, piercing
the water. They appeared united, inexorably bound to a common
fate. How comes this unity?"
--Anonymous, 17th century (from Shaw)
For a bird to participate in a flock, it must have behaviors that allow it to coordinate its movements with those of its flockmates. These behaviors are not particularly unique; all creatures have them to some degree. Natural flocks seem to consist of two balanced, opposing behaviors: a desire to stay close to the flock and a desire to avoid collisions within the flock [34]. It is clear why an individual bird wants to avoid collisions with its flockmates. But why do birds seem to seek out the airborne equivalent of a nasty traffic jam? The basic urge to join a flock seems to be the result of evolutionary pressure from several factors: protection from predators, statistically improving survival of the (shared) gene pool from attacks from predators, profiting from a larger effective search pattern in the quest for food, and advantages for social and mating activities [33].
There is no evidence that the complexity of natural flocks is bounded in any way. Flocks do not become "full" or "overloaded" as new birds join. When herring migrate toward their spawning grounds, they run in schools extending as long as 17 miles and containing millions of fish [32]. Natural flocks seem to operate in exactly the same fashion over a huge range of flock populations. It does not seem that an individual bird can be paying much attention to each and every one of its flockmates. But in a huge flock spread over vast distances, an individual bird must have a localized and filtered perception of the rest of the flock. A bird might be aware of three categories: itself, its two or three nearest neighbors, and the rest of the flock [23].
These speculations about the "computational complexity" of flocking are meant to suggest that birds can flock with any number of flockmates because they are using what would be called in formal computer science a constant time algorithm. That is, the amount of "thinking" that a bird has to do in order to flock must be largely independent of the number of birds in the flock. Otherwise we would expect to see a sharp upper bound on the size of natural flocks when the individual birds became overloaded by the complexity of their navigation task. This has not be observed in nature.
Contrast the insensitivity to complexity of real flocks with the situation for the simulated flocks described below. The complexity of the flocking algorithm described is basically O(N 2 ). That is, the work required to run the algorithm grows as the square of the flock's population. We definitely do see an upper bound on the size of simulated flocks implemented as described here. Some techniques to address this performance issue are discussed in the section Algorithmic Considerations.
To build a simulated flock, we start with a boid model that supports geometric flight. We add behaviors that correspond to the opposing forces of collision avoidance and the urge to join the flock. Stated briefly as rules, and in order of decreasing precedence, the behaviors that lead to simulated flocking are:
Velocity is a vector quantity, referring to the combination of heading and speed. The manner in which the results from each of these behaviors is reconciled and combined is significant and is discussed in more detail later. Similarly, the meaning nearby in these rules is key to the flocking process. This is also discussed in more detail later, but generally one boid's awareness of another is based on the distance and direction of the offset vector between them.
Static collision avoidance and dynamic velocity matching are complementary. Together they ensure that the members of a simulated flock are free to fly within the crowded skies of the flock's interior without running into one another. Collision avoidance is the urge to steer a way from an imminent impact. Static collision avoidance is based on the relative position of the flockmates and ignores their velocity. Conversely, velocity matching is based only on velocity and ignores position. It is a predictive version of collision avoidance: if the boid does a good job of matching velocity with its neighbors, it is unlikely that it will collide with any of them any time soon. With velocity matching, separations between boids remains approximately invariant with respect to ongoing geometric flight. Static collision avoidance serves to establish the minimum required separation distance; velocity matching tends to maintain it.
Flock centering makes a boid want to be near the center of the flock. Because each boid has a localized perception of the world. "center of the flock" actually means the center of the nearby flockmates. Flock centering causes the boid to fly in a direction that moves it closer to the centroid of the nearby boids. if a boid is deep inside a flock, the population density in its neighborhood is roughly homogeneous; the boid density is approximately the same in all directions. In this case, the centroid of the neighborhood boids is approximately at the center of the neighborhood, so the flock centering urge is small. But if a boid is on the boundary of the flock, its neighboring boids are on one side. The centroid of the neighborhood boids is displaced from the center of the neighborhood toward the body of the flock. Here the flock centering urge is stronger and the flight path will be deflected somewhat toward the local flock center.
Real flocks sometimes split apart to go around an obstacle. To be realistic, the simulated flock model must also have this ability. Flock centering correctly allows simulated flocks to bifurcate. As long as an individual boid can stay close to its nearby neighbors, it does not care if the rest of the flock turns away. More simplistic models proposed for flock organization (such as a central force model or a follow the designated leader model) do not allow splits.
The flock model presented here is actually a better model of a school or a herd than a flock. Fish in murky water (and land animals with their inability to see past their herdmates) have a limited, short-range perception of their environment. Birds, especially those on the outside of a flock, have excellent long-range "visual perception." Presumably this allows widely separated flocks to join together. If the flock centering urge was completely localized, when two flocks got a certain distance apart they would ignore each other. Long-range vision seems to play a part in the incredibly rapid propagation of a maneuver wave" through a flock of birds. It has been shown that the speed of propagation of this wavefront reaches three times the speed implied by the measured startle reaction time of the individual birds. The explanation advanced by Wayne Potts is that the birds perceive the motion of the oncoming "maneuver wave" and time their own turn to match it [25]. Potts refers to this as the "chorus line" hypothesis.
The three behavioral urges associated with flocking (and others to be discussed below) each produce an isolated suggestion about which way to steer the boid. These are expressed as acceleration requests. Each behavior says: "if I were in charge, I would accelerate in that direction." The acceleration request is in terms of a 3D vector that, by system convention, is truncated to unit magnitude or less. Each behavior has several parameters that control its function; one is a "strength," a fractional value between zero and one that can further attenuate the acceleration request. It is up to the navigation module of the boid brain to collect all relevant acceleration requests and then determine a single behaviorally desired acceleration. It must combine, prioritize, and arbitrate between potentially conflicting urges. The pilot module takes the acceleration desired by the navigation module and passes it to the flight module, which attempts to fly in that direction.
The easiest way to combine acceleration requests is to average them. Because of the included "strength" factors, this is actually a weighted average. The relative strength of one behavior to another can be defined this way, but it is a precarious interrelationship that is difficult to adjust. An early version of the boid model showed that navigation by simple weighted averaging of acceleration requests works "pretty well." A boid that chooses its course this way will fly a reasonable course under typical conditions. But in critical situations, such as potential collision with obstacles, conflicts must be resolved in a timely manner. During high-speed flight, hesitation or indecision is the wrong response to a brick wall dead ahead.
The main cause of indecision is that each behavior might be shouting advice about which way to turn to avoid disaster, but if those acceleration requests happen to lie in approximately opposite directions, they will largely cancel out under a simple weighted averaging scheme. The boid would make a very small turn and so continue in the same direction, perhaps to crash into the obstacle. Even when the urges do not cancel out, averaging leads to other problems. Consider flying over a gridwork of city streets between the skyscrapers; while "fly north" or "fly east" might be good ideas, it would be a bad idea to combine them as "fly northeast."
Techniques from artificial intelligence, such as expert systems, can be used to arbitrate conflicting opinions. However, a less complex approach is taken in the current implementation. Prioritized acceleration allocation is based on a strict priority ordering of all component behaviors, hence of the consideration of their acceleration requests. (This ordering can change to suit dynamic conditions.) The acceleration requests are considered in priority order and added into an accumulator. The magnitude of each request is measured and added into another accumulator. This process continues until the sum of the accumulated magnitudes gets larger than the maximum acceleration value, which is a parameter of each boid. The last acceleration request is trimmed back to compensate for the excess of accumulated magnitude. The point is that a fixed amount of acceleration is under the control of the navigation module; this acceleration is parceled out to satisfy the acceleration request of the various behaviors in order of priority. In an emergency the acceleration would be allocated to satisfy the most pressing needs first; if all available acceleration is "used up," the less pressing behaviors might be temporarily unsatisfied. For example. the flock centering urge could be correctly ignored temporarily in favor of a maneuver to avoid a static obstacle.
The boid model does not directly simulate the senses used by real animals during flocking (vision and hearing) or schooling (vision and fishes' unique "lateral line" structure that provides a certain amount of pressure imaging ability [23, 24]). Rather the perception model tries to make available to the behavior model approximately the same information that is available to a real animal as the end result of its perceptual and cognitive processes.
This is primarily a matter of filtering out the surplus information that is available to the software that implements the boid's behavior. Simulated boids have direct access to the geometric database that describes the exact position, orientation, and velocity of all objects in the environment. The real bird's information about the world is severely limited because it perceives through imperfect senses and because its nearby flockmates hide those farther away. This is even more pronounced in herding animals because they are all constrained to be in the same plane. In fish schools. visual perception of neighboring fish is further limited by the scattering and absorption of light by the sometimes murky water between them These factors combine to strongly localize the information available to each animal.
Not only is it unrealistic to give each simulated boid perfect and complete information about the world, it is just plain wrong and leads to obvious failures of the behavior model. Before the current implementation of localized flock centering behavior was implemented. the flocks used a central force model. This leads to unusual effects such as causing all members of a widely scattered flock to simultaneously converge toward the flock's centroid. An interesting result of the experiments reported in this paper is that the aggregate motion that we intuitively recognize as "flocking" (or schooling or herding) depends upon a limited, localized view of the world.
The behaviors that make up the flocking model are stated in terms of "nearby flockmates." In the current implementation, the neighborhood is defined as a spherical zone of sensitivity centered at the boid's local origin. The magnitude of the sensitivity is defined as an inverse exponential of distance. Hence the neighborhood is defined by two parameters: a radius and exponent. There is reason to believe that this field of sensitivity should realistically be exaggerated in the forward direction and probably by an amount proportional to the boid's speed. Being in motion requires an increased awareness of what lies ahead, and this requirement increases with speed. A forward-weighted sensitivity zone would probably also improve the behavior in the current implementation of boids at the leading edge of a flock, who tend to get distracted by the flock behind them. Because of the way their heads and eyes are arranged, real birds have a wide field of view (about 300 degrees), but the zone of overlap from both eyes is small (10 to 15 degrees). Hence the bird has stereo depth perception only in a very small, forward-oriented cone. Research is currently under way on models of forward-weighted perception for boids.
In an early version of the flock model, the metrics of attraction and repulsion were weighted linearly by distance. This spring-like model produced a bouncy flock action, fine perhaps for a cartoony characterization, but not very realistic. The model was changed to use an inverse square of the distance. This more gravity-like model produced what appeared to be a more natural, better damped flock model. This correlated well with the carefully controlled quantitative studies that Brian Partridge made of the spatial relationships of schooling fish [23]; he found that "a fish is much more strongly influenced by its near neighbors than it is by the distant members of the school. The contribution of each fish to the [influence] is inversely proportional to the square or the cube of the distance." In previous work he and colleagues [23, 24] demonstrated that fishes school based on information from both their visual system and from their "lateral line" organ which senses pressure waves. The area of a perspective image of the silhouette of an object (its "visual angle") varies inversely with the square of its distance, and that pressure waves traveling through a 3D medium like water fall off inversely with the cube of the distance.
The boid perception model is quite ad hoc and avoids actually simulating vision. Artificial vision is an extremely complex problem [38] and is far beyond the scope of this work. But if boids could "see" their environment, they would be better at path planning than the current model. It is possible to construct simple maze like shapes that would confuse the current boid model but would be easily solved by a boid with vision.
The flocking model described above gives boids an eagerness to participate in an acceptable approximation of flock like motion. Boids released near one another begin to flock together, cavorting and jostling for position. The boids stay near one another (flock centering) but always maintain prudent separation from their neighbors' (collision avoidance), and the flock quickly becomes "polarized"-its members heading in approximately the same direction at approximately the same speed (velocity marching); when they change direction they do it in synchronization. Solitary boids and smaller flocks join to become larger flocks, and in the presence of external obstacles (discussed below), larger flocks can split into smaller flocks.
For each simulation run, the initial position (within a specified ellipsoid), heading, velocity, and various other parameters of the boid model are initialized to values randomized within specified distributions. A restartable random number generator is used to allow repeatability. This randomization is not required; the boids could just as well start out arranged in a regular pattern, all other aspects of the flock model are completely deterministic and repeatable.
When the simulation is run, the flock's first action is a reaction to the initial conditions. If the boids started out too closely crowded together, there is an initial "flash expansion" where the mutual desire to avoid collision drives the boids radially away from the site of the initial over-pressure. If released in a spherical shell with a radius smaller than the "neighborhood" radius, the boids contract toward the sphere's center; otherwise they begin to coalesce into small flockettes that might themselves begin to join together. If the boids are confined within a certain region, the smaller flocks eventually conglomerate into a single flock if left to wander long enough.
The behaviors discussed so far provide for the ability of individual birds to fly and participate in happy aimless flocking. But to combine flock simulations with other animated action, we need more direct control over the flock. We would like to direct specific action at specific times (for example, "the flock enters from the left at :02.3 seconds into the sequence, turns to fly directly upward at :03.5, and is out of the frame at :04.0").
The current implementation of the boid model has several facilities to direct the motion and timing of the flock action. First, the simulations are run under the control of a general-purpose animation scripting system [36]. The details of that scripting system are not relevant here except that, in addition to the typical interactive motion control facilities, it provides the ability to schedule the invocation of user-supplied software (such as the flock model) on a frame-by-frame basis. This scripting facility is the basic tool used to describe the timing of various flock actions. It also allows flexible control over the time-varying values of parameters, which can be passed down to the simulation software. Finally the script is used to set up and animate all nonbehavioral aspects of the scene, such as backgrounds, lighting, camera motion, and other visible objects.
The primary tool for scripting the flock's path is the migratory urge built into the boid model. In the current model this urge is specified in terms of a global target, either as a global direction (as in "going Z for the winter") or as a global position-a target point toward which all birds fly. The model computes a bounded acceleration that incrementally turns the boid toward its migratory target.
With the scripting system. we can animate a dynamic parameter whose value is. a global position vector or a global direction vector. This parameter can be passed to the flock, which can in turn pass it along to all boids, each of which sets its own "migratory goal register." Hence the global migratory behavior of all birds can be directly controlled from the script. (Of course, it is not necessary to alter all boids at the same time, for example, the delay could be a function of their present position in space. Real flocks do not change direction simultaneously [25], but rather the turn starts with a single bird and spreads quickly across the flock like a shock wave.)
We can lead the flock around by animating the goal point along the desired path, somewhat ahead of the flock. Even if the migratory goal point is changed abruptly the path of each boid still is relatively smooth because of the flight model's simulated conservation of momentum. This means that the boid's own flight dynamics implement a form of smoothing interpolation between "control points."
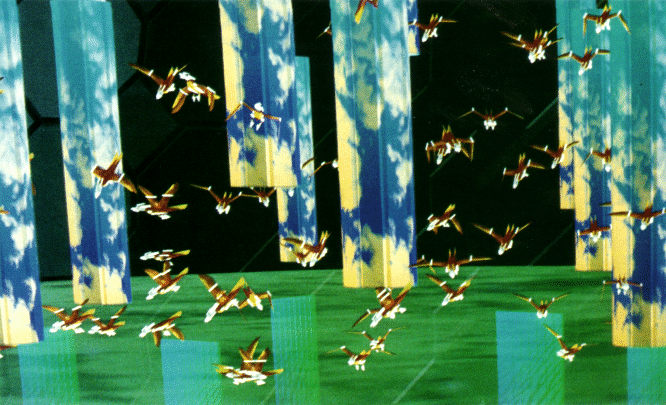
The most interesting motion of a simulated flock comes from interaction with other objects in the environment. The isolated behavior of a flock tends to reach a steady state and becomes rather sterile. The flock can be seen as a relaxation solution to the constraints implied by its behaviors. For example, the conflicting urges of flock centering and collision avoidance do not lead to constant back and forth motion, but rather the boids eventually strike a balance between the two urges (the degree of damping controls how soon this balance is reached). Environmental obstacles and the boid's attempts to navigate around them increase the apparent complexity of the behavior of the flock. (In fact the complexity of real flocks might be due largely to the complexity of the natural environment.)
Environmental obstacles are also important from the standpoint of modeling the scene in which we wish to place the flock. If the flock is scripted to fly under a bridge and around a tree, we must be able to represent the geometric shape and dimension of these obstacles. The approach taken here is to independently model the "shape for rendering" and the "shape for collision avoidance." The types of shapes currently used for environmental obstacles are much less complicated than the models used for rendering of computer graphic models. The current work implements two types of shapes of environmental collision avoidance. One is based on the force field concept, which works in undemanding situations but has some shortcomings. The other model called steer-to-avoid is more robust and seems closer in spirit to the natural mechanism.
The force field model postulates a field of repulsion force emanating from the obstacle out into space; the boids are increasingly repulsed as they get closer to the obstacle. This scheme is easy to model; the geometry of the field is usually fairly simple and so an avoidance acceleration can be directly calculated from the field equation. These models can produce good results, such as in "Eurythmy" [4], but they also have drawbacks that are apparent on close examination. If a boid approaches an obstacle surrounded by a force field at an angle such that it is exactly opposite to the direction of the force field, the boid will not turn away. In this case the force field serves only to slow the boid by accelerating it backwards and provides no side thrust at all. The worst reaction to an impending collision is to fail to turn. Force fields also cause problems with "peripheral vision." The boid should notice and turn away from a wall as it flies toward it, but the wall should be ignored if the boid is flying alongside it. Finally, force fields tend to be too strong close up and too weak far away; avoiding an obstacle should involve long-range planning rather than panicky corrections at the last minute.
Steer-to-avoid is a better simulation of a natural bird guided by vision. The boid considers only obstacles directly in front of it. (It finds the intersection, if any, of its local Z axis with the obstacle.) Working in local perspective space, it finds the silhouette edge of the obstacle closest to the point of eventual impact. A radial vector is computed which will aim the boid at a point one body length beyond that silhouette edge (see figure 2). Currently steer-to avoid has been implemented for several obstacle shapes: spheres, cylinders, planes, and boxes. Collision avoidance for arbitrary convex polyhedral obstacles is being developed.
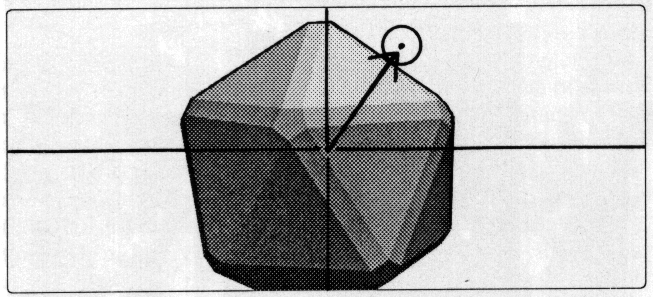
Figure 2.
Obstacles are not necessarily fixed in space; they can be animated around by the script during the animation. Or more interestingly, the obstacles can be behavioral characters. Sparrows might flock around a group of obstacles that is in fact a herd of elephants. Similarly, behavioral obstacles might not merely be in the way; they might be objects of fear such as predators. It has been noted [25] that natural flocking instincts seem to be sharpened by predators.
The model of polarized noncolliding aggregate motion has many applications, visual simulation of bird flocks in computer animation being one. Certain modifications yield a fish school model. Further modifications, such as [imitation to a 2D surface and the ability to follow the terrain, lead to a herd model. Imagine a herd of PODA-style legged creatures [9], using Karl Sims' techniques for locomotion over uneven, complex terrain [35]. Other applications are less obvious. Traffic patterns, such as the flow of cars on a freeway, is a flock-like motion. There are specialized behaviors, such as being constrained to drive within the lanes, but the basic principles that keep boids from colliding are just as applicable on the freeway. We could imagine creating crowds of "extras" (human or otherwise) for feature films. However the most fun are the offbeat combinations possible in computer graphics by mixing and matching: a herd of pogo sticks, a flock of Pegasus-like winged horses, or a traffic jam of spaceships on a 3D interplanetary highway.
One serious application would be to aid in the scientific investigation of flocks, herds, and schools. These scientists must work almost exclusively in the observational mode; experiments with natural flocks and schools are difficult to perform and are likely to disturb the behaviors under study. It might be possible, using a more carefully crafted model of the realistic behavior of a certain species of bird, to perform controlled and repeatable experiments with "simulated natural flocks." A theory of flock organization can be unambiguously tested by implementing a distributed behavioral model and simply comparing the aggregate motion of the simulated flock with the natural one.
A naive implementation of the basic flocking algorithm would grow in complexity as the order of the square of the flock's population ("O(N2)"). Basically this is because each boid must reason about each of the other boids, even if only to decide to ignore it. This does not say the algorithm is slow or fast, merely that as the size of the problem (total population of the flock) increases, the complexity increases even faster. Doubling the number of boids quadruples the amount of time taken.
However, as stated before, real birds are probably not as sensitive to the total flock population. This gives hope that the simulated boid could be taught to navigate independently of the total population. Certainly part of the problem is that we are trying to run the simulation of the whole flock on a single computer. The natural solution is to use distributed processing, as the real flock does. If we used a separate processor for each boid, then even the naive implementation of the flocking algorithm would be O(N), or linear with respect to the population. But even that is not good enough. It still means that as more boids are added to the flock, the complexity of the problem increases.
What we desire is a constant time algorithm, one that is insensitive to the total population. Another way to say this is that an N2 algorithm would be OK if there was an efficient way to keep N very small. Two approaches to this goal are currently under investigation. One is dynamic spatial partitioning of the flock; the boids are sorted into a lattice of "bins" based on their position in space. A boid trying to navigate inside the flock could get quick access to the flockmates that are physically nearby by examining the "bins" near its current position. Another approach is to do incremental collision detection (x`nearness testing"). General collision detection is another N2 algorithm, but if one does collision detection incrementally, based on a partial solution that described the situation just a moment before, then the algorithm need worry only about the changes and so can run much faster, assuming that the incremental changes are small. The incremental collision detection algorithm used in Girard's PODA system [9] apparently achieves constant time performance in the typical case.
The boids software was written in Symbolics Common Lisp. The code and animation were produced on a Symbolics 3600 Lisp Machine, a high-performance personal computer. The flock software is implemented in Flavors, the object-oriented programming extensions to Symbolics Common Lisp. The geometric aspects of the system are layered upon S-Geometry, an interactive geometric modeler [37]. Boids are based on the flavor 3D:OBJECT, which provides their geometric abilities. The flock simulations are invoked from scripts created and animated with the S Dynamics [36] animation system, which also provided the real-time playback facility used to view the motion tests. The availability of this graphical toolkit allowed the author to focus immediately on the issues unique to this project. One example of the value of this substrate is that the initial version of the flock model, including implementation, testing, debugging, and the production of seven short motion tests was accomplished in the ten days before the SIGGRAPH `86 conference.
The boid software has not been optimized for speed. But this report would be incomplete without a rough estimate of the actual performance of the system. With a flock of 80 boids, using the naive O(N2) algorithm (and so 6400 individual boid-to-boid comparisons), on a single Lisp Machine without any special hardware accelerators, the simulation ran for about 95 seconds per frame. A ten-second (300 frame) motion test took about eight hours of real time to produce.
This paper has largely ignored the internal animation of the geometrical model that provides the visual representation of the boid. The original motion tests produced with these models all show flocks of little abstract rigid shapes that might be paper airplanes. There was no flapping of wings nor turning of heads. and there was certainly no character animation. These topics are all important and pertinent to believable animation of simulated flocks. But the underlying abstract nature of flocking as polarized. noncolliding aggregate motion is largely independent of these issues of internal shape change and articulation. This notion is supported by the fact that most viewers of these simulations identify the motion of these abstract objects as "flocking" even in the absence of any internal animation.
But doing a believable job of melding these two aspects of the motion is more than a matter of concatenating the action of an internal animation cycle for the character with the motion defined by geometrical flight. There are important issues of synchronization between the current state of the flight dynamics model, and the amplitude and frequency of the wing motion cycle. Topics of current development include internal animation. synchronization, and interfaces between the simulation-based flock model and other more traditional. interactive animation scripting systems. We would like to allow a skilled computer animator to design a bird character and define its "wing flap cycle" using standard interactive modeling and scripting techniques. and then be able to take this cyclic motion and "plug it in" to the flock simulation model causing the boids in the flock to fly according to the scripted cycle.
The behaviors that have been discussed in this paper are all simplistic, isolated behaviors of low complexity. The boids have a geometric and kinematic state. but they have no significant mental state. Real animals have more elaborate, abstract behaviors than a simple desire to avoid a painful collision: they have more complex motivations than a simple desire to fly to a certain point in space. More interesting behavior models would take into account hunger, finding food, fear of predators, a periodic need to sleep, and so on. Behavior models of this type have been created by other investigators [6, 19, 21], but they have not yet been implemented for the boid model described here.
This paper has presented a model of polarized. noncolliding aggregate motion. such as that of flocks. herds. and schools. The model is based on simulating the behavior of each bird independently. Working independently. the birds try both to stick together and avoid collisions with one another and with other objects in their environment. The animations showing simulated flocks built from this model seem to correspond to the observer's intuitive notion of what constitutes "flock-like motion." However it is difficult to objectively measure how valid these simulations are. By comparing behavioral aspects of the simulated flock with those of natural flocks. we are able improve and refine the model. But having approached a certain level of realism in the model. the parameters of the simulated flock can be altered at will by the animator to achieve many variations on flock-like behavior.
I would like to thank flocks. herds. and schools for existing; nature is the ultimate source of inspiration for computer graphics and animation. I would also like to acknowledge the contributions to this research provided by workers in a wonderfully diverse collection of pursuits:
To the natural sciences of behavior, evolution, and zoology: for doing the hard work, the Real Science, on which this computer graphics approximation is based. To the Logo group who invented the appropriate geometry, and so put us in the driver's seat. To the Actor semantics people who invented the appropriate control structure, and so gave the boid a brain. To the many developers of modern Lisp who invented the appropriate programming language. To my past and present colleagues at MIT, III, and Symbolics who have patiently listened to my speculations about flocks for years and years before I made my first boid fly. To the Graphics Division of Symbolics, Inc., who employ me, put up with my nasty disposition, provide me with fantastic computing and graphics facilities, and have generously supported the development of the work described here. And to the field of computer graphics, for giving professional respectability to advanced forms of play such as reported in this paper.

Freeman and Company. San Francisco, 1970, pp. 452480.
Permission to copy without fee all or part of this material is granted provided that the copies are not made or distributed for direct commercial advantage, the ACM copyright notice and the title of the publication and its date appear, and notice is given that copying is by permission of the Association for Computing Machinery. To copy otherwise, or to republish requires a fee and/or specific permission.
(C)1987 ACM-0-89791-227-6/87/007/0025 $00.75