



Next: obv : Optimization for
Up: AUTO Demos : Optimization.
Previous: opt : A Model
Contents
ops : Optimization of Periodic Solutions.
This demo illustrates the method of successive continuation
for the optimization of periodic solutions.
For a detailed description of the basic method see
DoKeKe:91b DoKeKe:91b.
The illustrative system of autonomous ODEs, taken from
Alej:91 Alej:91, is
 |
(17.1) |
with objective functional
where
 .
Thus, in this application, a one-parameter extremum of
.
Thus, in this application, a one-parameter extremum of  corresponds
to a fold with respect to the problem parameter
corresponds
to a fold with respect to the problem parameter  ,
and multi-parameter extrema correspond to generalized folds.
Note that, in general, the objective functional is an integral along
the periodic orbit, so that a variety of optimization problems
can be addressed.
,
and multi-parameter extrema correspond to generalized folds.
Note that, in general, the objective functional is an integral along
the periodic orbit, so that a variety of optimization problems
can be addressed.
For the case of periodic solutions, the extended optimality system
can be generated automatically, i.e., one need only define the vector field
and the objective functional, as in done in the file ops.f.
For reference purpose it is convenient here to write down
the full extended system in its general form :
 |
(17.2) |
Above 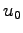 is a reference solution, namely, the previous solution along
a solution family.
is a reference solution, namely, the previous solution along
a solution family.
In the computations below, the two preliminary runs, with IPS=1 and IPS=2,
respectively, locate periodic solutions.
The subsequent runs are with IPS=15 and hence use the automatically
generated extended system.
- -
- Run 1. Locate a Hopf bifurcation.
The free system parameter is
 .
.
- -
- Run 2.
Compute a family of periodic solutions from the Hopf bifurcation.
- -
- Run 3.
This run retraces part of the periodic solution family,
using the full optimality system,
but with all adjoint variables,
 ,
and hence
,
and hence 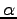 , equal to zero.
The optimality parameters
, equal to zero.
The optimality parameters  and
and  are zero throughout.
An extremum of the objective functional with respect to
are zero throughout.
An extremum of the objective functional with respect to  is located.
Such a point corresponds to a branch point of the extended system.
Given the choice of objective functional in this demo,
this extremum is also a fold with respect to
is located.
Such a point corresponds to a branch point of the extended system.
Given the choice of objective functional in this demo,
this extremum is also a fold with respect to  .
.
- -
- Run 4.
Branch switching at the above-found branch point yields nonzero
values of the adjoint variables.
Any point on the bifurcating family away from the branch point
can serve as starting solution for the next run.
In fact, the branch-switching can be viewed as generating
a nonzero eigenvector in an eigenvalue-eigenvector relation.
Apart from the adjoint variables, all other variables remain
unchanged along the bifurcating family.
- -
- Run 5.
The above-found starting solution is continued in two system parameters,
here
 and
and  ; i.e., a two-parameter family
of extrema with respect to
; i.e., a two-parameter family
of extrema with respect to  is computed.
Along this family the value of the optimality parameter
is computed.
Along this family the value of the optimality parameter  is monitored, i.e., the value of the functional that vanishes
at an extremum with respect to the system parameter
is monitored, i.e., the value of the functional that vanishes
at an extremum with respect to the system parameter  .
Such a zero of
.
Such a zero of  is, in fact, located, and hence an extremum
of the objective functional with respect to both
is, in fact, located, and hence an extremum
of the objective functional with respect to both  and
and
 has been found.
Note that, in general,
has been found.
Note that, in general,  is the value of the
functional that vanishes at an extremum with respect to the system
parameter
is the value of the
functional that vanishes at an extremum with respect to the system
parameter  .
.
- -
- Run 6.
In the final run, the above-found two-parameter extremum is continued
in three system parameters, here
 ,
,  ,
and
,
and  , toward
, toward
 .
Again, given the particular choice of objective functional,
this final continuation has an alternate significance here :
it also represents a three-parameter family of transcritical
secondary periodic bifurcations points.
.
Again, given the particular choice of objective functional,
this final continuation has an alternate significance here :
it also represents a three-parameter family of transcritical
secondary periodic bifurcations points.
Although not illustrated here, one can restart an ordinary
continuation of periodic solutions, using IPS=2 or IPS=3,
from a labeled solution point on a family computed with IPS=15.
The free scalar variables specified in the AUTO constants-files
for Run 3 and Run 4 are shown in Table 17.2.
Table 17.2:
Runs 3 and 4 (files c.ops.3 and c.ops.4).
| Index |
3 |
11 |
12 |
22 |
-22 |
-23 |
-31 |
| Variable |
 |
 |
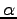 |
 |
![$ [\lambda_2]$](img303.png) |
![$ [\lambda_3]$](img304.png) |
![$ [T]$](img305.png) |
|
The parameter 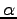 , which is the norm of the adjoint variables,
becomes nonzero after branch switching in Run 4.
The negative indices (-22, -23, and -31) set the active optimality
functionals, namely for
, which is the norm of the adjoint variables,
becomes nonzero after branch switching in Run 4.
The negative indices (-22, -23, and -31) set the active optimality
functionals, namely for  ,
,  , and
, and  , respectively,
with corresponding variables
, respectively,
with corresponding variables  ,
,  , and
, and  ,
respectively.
These should be set in the first run with IPS=15 and remain unchanged
in all subsequent runs.
,
respectively.
These should be set in the first run with IPS=15 and remain unchanged
in all subsequent runs.
Table 17.3:
Run 5 (file c.ops.5).
| Index |
3 |
2 |
11 |
22 |
-22 |
-23 |
-31 |
| Variable |
 |
 |
 |
 |
![$ [\lambda_2]$](img303.png) |
![$ [\lambda_3]$](img304.png) |
![$ [T]$](img305.png) |
|
In Run 5 the parameter 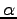 , which has been replaced by
, which has been replaced by  ,
remains fixed and nonzero.
The variable
,
remains fixed and nonzero.
The variable  monitors the value of the optimality functional
associated with
monitors the value of the optimality functional
associated with  .
The zero of
.
The zero of  located in this run signals an extremum
with respect to
located in this run signals an extremum
with respect to  .
.
Table 17.4:
Run 6 (file c.ops.6).
| Index |
3 |
2 |
1 |
11 |
-22 |
-23 |
-31 |
| Variable |
 |
 |
 |
 |
![$ [\lambda_2]$](img303.png) |
![$ [\lambda_3]$](img304.png) |
![$ [T]$](img305.png) |
|
In Run 6  , which has been replaced by
, which has been replaced by  , remains zero.
, remains zero.
Note that  and
and  are not used as variables in any
of the runs; in fact, their values remain zero throughout.
Also note that the optimality functionals corresponding to
are not used as variables in any
of the runs; in fact, their values remain zero throughout.
Also note that the optimality functionals corresponding to
 and
and  (or, equivalently, to
(or, equivalently, to  and
and  )
are active in all runs.
This set-up allows the detection of the extremum of the objective functional,
with
)
are active in all runs.
This set-up allows the detection of the extremum of the objective functional,
with  and
and  as scalar equation parameters,
as a bifurcation in the third run.
as scalar equation parameters,
as a bifurcation in the third run.
The parameter  , and its corresponding optimality variable
, and its corresponding optimality variable  ,
are not used in this demo.
Also,
,
are not used in this demo.
Also,  is used in the last run only, and its corresponding
optimality variable
is used in the last run only, and its corresponding
optimality variable  is never used.
is never used.
Table 17.5:
Commands for running demo ops.
| AUTO -COMMAND |
ACTION |
| ! mkdir ops |
create an empty work directory |
| cd ops |
change directory |
| demo('ops') |
copy the demo files to the work directory |
| run(c='ops.1') |
locate a Hopf bifurcation |
| sv('0') |
save output-files as b.0, s.0, d.0 |
| run(c='ops.2',s='0') |
compute a family of periodic solutions; restart from s.0. Constants changed : IPS, IRS, NMX, NUZR
|
| ap('0') |
append the output-files to b.0, s.0, d.0 |
| run(c='ops.3',s='0') |
locate a 1-parameter extremum as a bifurcation; restart from s.0. Constants changed : IPS, IRS, ICP, 
|
| sv('1') |
save the output-files as b.1, s.1, d.1 |
| run(c='ops.4',s='1') |
switch branches to generate optimality starting data; restart from s.1. Constants changed : IRS, ISP, ISW, NMX
|
| ap('1') |
append the output-files to b.1, s.1, d.1 |
| run(c='ops.5',s='1') |
compute 2-parameter family of 1-parameter extrema; restart from s.1. Constants changed : IRS, ISW, ICP, ISW, 
|
| sv('2') |
save the output-files as b.2, s.2, d.2 |
| run(c='ops.6',s='2') |
compute 3-parameter family of 2-parameter extrema; restart from s.2. Constants changed : IRS, ICP, EPSL, EPSU, NUZR
|
| sv('3') |
save the output-files as b.3, s.3, d.3 |
|




Next: obv : Optimization for
Up: AUTO Demos : Optimization.
Previous: opt : A Model
Contents
Gabriel Lord
2007-11-19




![]() , which is the norm of the adjoint variables,
becomes nonzero after branch switching in Run 4.
The negative indices (-22, -23, and -31) set the active optimality
functionals, namely for
, which is the norm of the adjoint variables,
becomes nonzero after branch switching in Run 4.
The negative indices (-22, -23, and -31) set the active optimality
functionals, namely for ![]() ,
, ![]() , and
, and ![]() , respectively,
with corresponding variables
, respectively,
with corresponding variables ![]() ,
, ![]() , and
, and ![]() ,
respectively.
These should be set in the first run with IPS=15 and remain unchanged
in all subsequent runs.
,
respectively.
These should be set in the first run with IPS=15 and remain unchanged
in all subsequent runs.
![]() , which has been replaced by
, which has been replaced by ![]() ,
remains fixed and nonzero.
The variable
,
remains fixed and nonzero.
The variable ![]() monitors the value of the optimality functional
associated with
monitors the value of the optimality functional
associated with ![]() .
The zero of
.
The zero of ![]() located in this run signals an extremum
with respect to
located in this run signals an extremum
with respect to ![]() .
.
![]() , which has been replaced by
, which has been replaced by ![]() , remains zero.
, remains zero.
![]() and
and ![]() are not used as variables in any
of the runs; in fact, their values remain zero throughout.
Also note that the optimality functionals corresponding to
are not used as variables in any
of the runs; in fact, their values remain zero throughout.
Also note that the optimality functionals corresponding to
![]() and
and ![]() (or, equivalently, to
(or, equivalently, to ![]() and
and ![]() )
are active in all runs.
This set-up allows the detection of the extremum of the objective functional,
with
)
are active in all runs.
This set-up allows the detection of the extremum of the objective functional,
with ![]() and
and ![]() as scalar equation parameters,
as a bifurcation in the third run.
as scalar equation parameters,
as a bifurcation in the third run.
![]() , and its corresponding optimality variable
, and its corresponding optimality variable ![]() ,
are not used in this demo.
Also,
,
are not used in this demo.
Also, ![]() is used in the last run only, and its corresponding
optimality variable
is used in the last run only, and its corresponding
optimality variable ![]() is never used.
is never used.