



Next: More Accuracy and Saddle-Node
Up: HomCont Demo : kpr.
Previous: Koper's Extended Van der
Contents
First, we locate a homoclinic orbit using
the homotopy method. The file kpr.f
already contains
approximate parameter values for a homoclinic orbit,
namely  PAR(1)=-1.851185,
PAR(1)=-1.851185,  PAR(2)=-0.15.
The files c.kpr.1 and h.kpr.1 specify the appropriate
constants for continuation in
PAR(2)=-0.15.
The files c.kpr.1 and h.kpr.1 specify the appropriate
constants for continuation in  =PAR(11) (also referred
to as PERIOD) and the dummy parameter
=PAR(11) (also referred
to as PERIOD) and the dummy parameter  =PAR(17)
starting
from a small solution in the local unstable manifold;
=PAR(17)
starting
from a small solution in the local unstable manifold;
make first
Among the output there is the line
BR PT TY LAB PERIOD L2-NORM ... PAR(17) ...
1 29 UZ 2 1.900184E+01 1.693817E+00 ... 4.433433E-09 ...
which indicates that a zero of the artificial parameter  has been located. This means that the right-hand end point of the solution
belongs to the plane that is tangent to the stable manifold at the saddle.
The output is stored in files b.1, s.1, d.1.
Upon plotting the data at label 2 (see Figure 23.1)
it can be noted that although the right-hand projection boundary
condition is satisfied, the solution is still quite away from the
equilibrium.
has been located. This means that the right-hand end point of the solution
belongs to the plane that is tangent to the stable manifold at the saddle.
The output is stored in files b.1, s.1, d.1.
Upon plotting the data at label 2 (see Figure 23.1)
it can be noted that although the right-hand projection boundary
condition is satisfied, the solution is still quite away from the
equilibrium.
The right-hand endpoint can be made to approach the
equilibrium by performing a further continuation in  with the
right-hand projection condition satisfied (PAR(17) fixed) but
with
with the
right-hand projection condition satisfied (PAR(17) fixed) but
with  allowed to vary.
allowed to vary.
Figure 23.1:
Projection on the 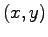 -plane of solutions
of the boundary value
problem with
-plane of solutions
of the boundary value
problem with
 .
.
 |
Figure 23.2:
Projection on the 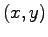 -plane of solutions of the
boundary value problem with
-plane of solutions of the
boundary value problem with  .
.
 |
make second
the output at label 4, stored in kpr.2,
BR PT TY LAB PERIOD L2-NORM ... PAR(1) ...
1 35 UZ 4 6.000000E+01 1.672806E+00 ... -1.851185E+00 ...
provides a good approximation to a homoclinic solution (see Figure
23.2).
The second stage to obtain a starting solution
is to add a solution to the modified adjoint
variational equation. This is achieved by setting both
ITWIST and ISTART to 1 (in h.kpr.3), which generates
a trivial guess for the adjoint equations. Because the adjoint
equations are linear, only a single
Newton step (by continuation in a trivial parameter)
is required to provide a solution.
Rather than choose a parameter that might be used internally
by AUTO , in c.kpr.3 we take the continuation parameter
to be PAR(11), which is not quite a trivial parameter
but whose affect upon the solution is mild.
make third
The output at the second point (label 6)
contains the converged homoclinic
solution (variables (U(1), U(2), U(3)) and the adjoint (U(4), U(5), U(6))). We now have a starting solution
and are ready to perform two-parameter continuation.
The fourth run
make fourth
continues the homoclinic orbit in PAR(1) and PAR(2).
Figure 23.3:
Projection on the 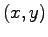 -plane of solutions
-plane of solutions  at 1 (
at 1 (
 ) and
2 (
) and
2 (
 ).
).
 |
Figure 23.4:
Three-dimensional blow-up of the solution curves
 at labels 1 (dotted) and 2 (solid line) from Figure 3.8.
at labels 1 (dotted) and 2 (solid line) from Figure 3.8.
 |
Note that several other parameters appear in
the output. PAR(10) is a dummy parameter
that should be zero when the adjoint is being computed correctly;
PAR(29), PAR(30), PAR(33) correspond to the
test functions 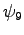 ,
,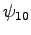 and
and  .
That these test functions were activated is specified
in three places in c.kpr.4 and h.kpr.4
as described in Section 20.6.
.
That these test functions were activated is specified
in three places in c.kpr.4 and h.kpr.4
as described in Section 20.6.
Note that at the end-point of
the family (reached when after NMX=50 steps) PAR(29) is
approximately zero which corresponds to a zero of 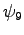 , a
non-central saddle-node homoclinic orbit. We shall return to the computation of
this codimension-two point later. Before reaching this point,
among the output we find two zeroes of PAR(33)
(test function
, a
non-central saddle-node homoclinic orbit. We shall return to the computation of
this codimension-two point later. Before reaching this point,
among the output we find two zeroes of PAR(33)
(test function  ) which gives the accurate
location of two inclination-flip bifurcations,
) which gives the accurate
location of two inclination-flip bifurcations,
BR PT TY LAB PAR(1) ... PAR(2) PAR(10) ... PAR(33)
1 6 UZ 10 -1.801662E+00 ... -2.002660E-01 -7.255434E-07 ... -1.425714E-04
1 12 UZ 11 -1.568756E+00 ... -4.395468E-01 -2.156353E-07 ... 4.514073E-07
That the test function really does have a regular zero at this point can
be checked from the data saved in b.3, plotting PAR(33) as
a function of PAR(1) or PAR(2).
Figure 23.3 presents solutions  of the modified adjoint
variational equation (for details see ChKuSa:95)
at parameter values on the homoclinic
family before and after the first detected inclination flip.
Note that these solutions were obtained by choosing a smaller
step DS and more output (smaller NPR) in
c.kpr.4.
A blow-up of the region close to the origin of this
figure is shown in Figure 23.4.
It illustrates the flip of the solutions of the adjoint equation while
moving through the bifurcation point. Note that the data in this
figure were plotted after first performing an additional
continuation of the solutions with respect to PAR(11).
of the modified adjoint
variational equation (for details see ChKuSa:95)
at parameter values on the homoclinic
family before and after the first detected inclination flip.
Note that these solutions were obtained by choosing a smaller
step DS and more output (smaller NPR) in
c.kpr.4.
A blow-up of the region close to the origin of this
figure is shown in Figure 23.4.
It illustrates the flip of the solutions of the adjoint equation while
moving through the bifurcation point. Note that the data in this
figure were plotted after first performing an additional
continuation of the solutions with respect to PAR(11).
Continuing in the other direction
make fifth
we approach a Bogdanov-Takens point
BR PT TY LAB PAR(1) ... PAR(10) ... PAR(33)
1 50 EP 13 -1.938276E+00 ... -7.523344E+00 ... 6.310810E+01
Figure 23.5:
Computed homoclinic orbits approaching the BT point
 |
Note that the numerical approximation has ceased to become reliable, since
PAR(10) has now become large.
Phase portraits of homoclinic orbits between the BT point and the first
inclination flip
are depicted in Figure 23.5. Note how the computed homoclinic orbits
approaching the BT point have their endpoints well away from the equilibrium.
To follow the homoclinic orbit to
the BT point with more precision, we would need to first perform continuation
in  (PAR(11)) to obtain a more accurate homoclinic solution.
(PAR(11)) to obtain a more accurate homoclinic solution.




Next: More Accuracy and Saddle-Node
Up: HomCont Demo : kpr.
Previous: Koper's Extended Van der
Contents
Gabriel Lord
2007-11-19
![]() with the
right-hand projection condition satisfied (PAR(17) fixed) but
with
with the
right-hand projection condition satisfied (PAR(17) fixed) but
with ![]() allowed to vary.
allowed to vary.

![]() , a
non-central saddle-node homoclinic orbit. We shall return to the computation of
this codimension-two point later. Before reaching this point,
among the output we find two zeroes of PAR(33)
(test function
, a
non-central saddle-node homoclinic orbit. We shall return to the computation of
this codimension-two point later. Before reaching this point,
among the output we find two zeroes of PAR(33)
(test function ![]() ) which gives the accurate
location of two inclination-flip bifurcations,
) which gives the accurate
location of two inclination-flip bifurcations,