An $R_1$-Reversible Homoclinic Solution.

The first run

make first

starts by copying the files rev.c.1 and rev.dat.1 to rev.f and rev.dat. The orbit contained in the data file is a ``primary'' homoclinic solution for $P=1.6$, with truncation (half-)interval PAR(11) = 39.0448429. which is reversible under $R_1$. Note that this reversibility is specified in h.rev.1 via NREV=1, (IREV(I), I=1,NDIM) = 0 1 0 1. Note also, from c.rev.1 that we only have one free parameter PAR(1) because symmetric homoclinic orbits in reversible systems are generic rather than of codimension one. The first run results in the output

  BR    PT  TY LAB    PAR(1)        L2-NORM       MAX U(1)   ...   
   1     7  UZ   2  1.700002E+00  2.633353E-01  4.179794E-01
   1    12  UZ   3  1.800000E+00  2.682659E-01  4.806063E-01
   1    15  UZ   4  1.900006E+00  2.493415E-01  4.429364E-01
   1    20  EP   5  1.996247E+00  1.111306E-01  1.007111E-01

which is consistent with the theoretical result that the solution tends uniformly to zero as $P\to 0$. Note, by plotting the data saved in s.1 that only ``half'' of the homoclinic orbit is computed up to its point of symmetry. See Figure 26.1.

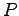Figure 26.1: $R_1$-Reversible homoclinic solutions on the half-interval $x/T \in [0,1]$ where $T=39.0448429$ for $P$ approaching $2$ (solutions with labels 1-5 respectively have decreasing amplitude)

Figure 26.2: $R_1$-reversible homoclinic orbits with oscillatory decay as $x \to -\infty$ (corresponding to label 6) and monotone decay (at label 10)

The second run continues in the other direction of PAR(1), with the test function $\psi_2$ activated for the detection of saddle to saddle-focus transition points

make second

The output

 BR  PT  TY LAB    PAR(1)        L2-NORM       MAX U(1)   ...    PAR(22)    
  1  11  UZ   6  1.000005E+00  2.555446E-01  1.767149E-01 ... -3.000005E+00
  1  22  UZ   7 -1.198325E-07  2.625491E-01  4.697314E-02 ... -2.000000E+00
  1  33  UZ   8 -1.000000E+00  2.741483E-01  4.316007E-03 ... -1.000000E+00
  1  44  UZ   9 -2.000000E+00  2.873838E-01  1.245735E-11 ...  2.318248E-08
  1  55  EP  10 -3.099341E+00  3.020172E-01 -2.749454E-11 ...  1.099341E+00

shows a saddle to saddle-focus transition (indicated by a zero of PAR(22)) at PAR(1)=-2. Beyond that label the first component of the solution is negative and (up to the point of symmetry) monotone decreasing. See Figure 26.2.