



Next: Bibliography
Up: HomCont Demo : Homoclinic
Previous: Branch switching for a
Contents
In ChGr:97 the following water wave model was considered:
![$\displaystyle \frac{2}{15}r''''-b r''+ar+\frac{3}{2}r^2- \frac{1}{2}(r')^2+[rr']' = 0.$](img598.png) |
(27.4) |
It represents solitary-wave solutions  ,
,  as
as
 of the 5th-order PDE
where
of the 5th-order PDE
where 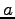 is the wave speed.
The ODE corresponds to a Hamiltonian system with Hamiltonian
and
System (27.4) is also reversible under the transformation
but we do not exploit the reversible structure (IREV=0), and
instead use it as an example of Hamiltonian system.
This system exhibits an orbit flip for a reversible Hamiltonian system.
In Hamiltonian systems, homoclinic orbits are codimension-zero
phenomena, and we have to add an additional parameter
is the wave speed.
The ODE corresponds to a Hamiltonian system with Hamiltonian
and
System (27.4) is also reversible under the transformation
but we do not exploit the reversible structure (IREV=0), and
instead use it as an example of Hamiltonian system.
This system exhibits an orbit flip for a reversible Hamiltonian system.
In Hamiltonian systems, homoclinic orbits are codimension-zero
phenomena, and we have to add an additional parameter  that breaks
the Hamiltonian structure in this system, by introducing artificial friction.
Thus, the actual system of equations that is
used for continuation is
where
that breaks
the Hamiltonian structure in this system, by introducing artificial friction.
Thus, the actual system of equations that is
used for continuation is
where
 and
and  is the usual skew symmetric matrix
in
is the usual skew symmetric matrix
in
 .
It is now possible to continue a homoclinic orbit in HomCont in two
parameters (
.
It is now possible to continue a homoclinic orbit in HomCont in two
parameters ( and either
and either 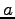 or
or 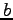 ); see also
Be:90a.
); see also
Be:90a.
An explicit solution exists for
 , and it is
given by
, and it is
given by
It corresponds to a reversible orbit flip for  (
( )
We start from this explicit solution, using ISTART=2, for
)
We start from this explicit solution, using ISTART=2, for  and
and
 :
:
demo('kdv')
ld('kdv')
rn()
sv('1')
BR PT TY LAB PAR(1) L2-NORM ... PAR(3)
1 1 EP 1 3.00000E+00 5.56544E+00 ... 0.00000E+00
1 2 EP 2 3.04959E+00 5.49141E+00 ... 1.77919E-17
Here PAR(1)=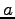 , PAR(2)=
, PAR(2)=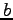 , and
PAR(3)=
, and
PAR(3)= . We have only done a
very small continuation to give AUTO a chance to create a good mesh
and avoid convergence problems later.
Next, we set ITWIST=1 and calculate the adjoint:
. We have only done a
very small continuation to give AUTO a chance to create a good mesh
and avoid convergence problems later.
Next, we set ITWIST=1 and calculate the adjoint:
rn(c='kdv.2',h='kdv.2',s='1')
sv('2')
BR PT TY LAB PAR(2) L2-NORM ... PAR(9)
1 2 EP 3 2.76556E+00 5.49140E+00 ... -7.62944E-08
We now need to move back to the orbit flip at  :
:
rn(c='kdv.3',h='kdv.3',s='2')
sv('3')
BR PT TY LAB PAR(1) L2-NORM ... PAR(3)
1 14 UZ 5 3.00000E+00 5.47612E+00 ... 1.47274E-09
Now all preparations are done to start homoclinic branch
switching. This is very similar to the technique used in
Sandstede's model in Section 27.1;
to find a 3-homoclinic orbit, we open 2 Lin gaps,
until  , while also varying
, while also varying  =PAR(3).
=PAR(3).
rn(c='kdv.4',h='kdv.4',s='3')
sv('4')
BR PT TY LAB PAR(3) ... PAR(21) PAR(22) PAR(24)
1 13 8 6.31458E-10 ... 1.65469E+01 -8.57681E-08 -7.30773E-07
1 23 UZ 9 1.46493E-09 ... 9.92489E+00 -5.84373E-12 1.93098E-07
1 26 10 4.01320E-09 ... 6.92406E+00 2.59555E-07 7.47534E-07
1 33 EP 11 2.15487E-06 ... 3.50000E+00 7.92587E-04 3.98390E-04
We then look for an orbit with  and close the gap corresponding
to
and close the gap corresponding
to
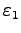 =PAR(22), for decreasing
=PAR(22), for decreasing 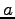 .
.
rn(c='kdv.5',h='kdv.5',s='4')
sv('5')
BR PT TY LAB PAR(2) ... PAR(3) PAR(22) PAR(24)
1 10 12 2.58030E+00 ... 2.15869E-06 7.65037E-04 3.82464E-04
1 13 UZ 13 2.32044E+00 ... 4.02730E-11 1.17522E-10 1.69655E-08
1 20 EP 14 -1.14985E-01 ... -8.87194E-04 -7.18231E-01 -3.31153E-01
and finally close the gap corresponding to
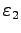 =PAR(24),
=PAR(24),
rn(c='kdv.6',h='kdv.6',s='5')
sv('6')
BR PT TY LAB PAR(2) ... PAR(3) PAR(23) PAR(24)
1 35 15 2.31893E+00 ... -2.16070E-08 7.69046E+00 -1.08126E-05
1 51 UZ 16 2.34039E+00 ... 2.83533E-07 3.47976E+00 1.42651E-04
1 58 UZ 17 3.08085E+00 ... 1.84952E-12 3.50004E+00 -1.64827E-10
1 70 EP 18 3.08870E+00 ... -8.10422E-08 5.87541E+00 -4.82991E-05
so that a three-homoclinic orbit is found. Here the zero at label
16 is the one we are looking for. At label 17, 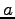 =PAR(1)
has changed
considerably to the extend that
=PAR(1)
has changed
considerably to the extend that  and a second 3-homoclinic orbit
is found. Note that for all zeros of PAR(24)=
and a second 3-homoclinic orbit
is found. Note that for all zeros of PAR(24)=
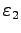 , the
parameter
, the
parameter  =PAR(3) is also zero (within AUTO accuracy),
which it has to be to remain
within the original Hamiltonian system.
Setting ISTART=1, a normal ``trivial'' continuation (with NMX=1)
of the orbit corresponding to label 16
lets HomCont produce a proper concatenated
3-homoclinic orbit:
=PAR(3) is also zero (within AUTO accuracy),
which it has to be to remain
within the original Hamiltonian system.
Setting ISTART=1, a normal ``trivial'' continuation (with NMX=1)
of the orbit corresponding to label 16
lets HomCont produce a proper concatenated
3-homoclinic orbit:
rn(c='kdv.7',h='kdv.7',s='6')
sv('7')
BR PT TY LAB PAR(2) L2-NORM ... PAR(3)
1 1 EP 19 2.34039E+00 7.51157E+00 ... 2.83533E-07
This 3-homoclinic orbit is depicted in Figure 27.6.
Figure 27.6:
A 3-homoclinic orbit in a 5th-order Hamiltonian
Korteweg-De Vries model.
|
|




Next: Bibliography
Up: HomCont Demo : Homoclinic
Previous: Branch switching for a
Contents
Gabriel Lord
2007-11-19
![$\displaystyle \frac{2}{15}r''''-b r''+ar+\frac{3}{2}r^2- \frac{1}{2}(r')^2+[rr']' = 0.$](img598.png)



![]() , and it is
given by
, and it is
given by
![$\displaystyle r(t)=3(b+\frac{1}{2})\mathrm{sech}^2\left([\frac{3}{4}(2b+1)]^{1/2}t\right).$](img611.png)