Question I: regexps

Which of the following matches regexp /abababa/?
1) abababa
2) aaba
3) aabbaa
4) aba
5) aabababa
Which of the following matches regexp /ab+c?/?
1) abc
2) ac
3) abbb
4) bbc
Which of the following matches regexp /a.[bc]+/?
1) abc
2) abbbbbbbb
3) azc
4) abcbcbcbc
5) ac
6) asccbbbbcbcccc
Which of the following matches regexp /abc|xyz/?
1) abc
2) xyz
3) abc|xyz
Which of the following matches regexp /[a-z]+[\.\?!]/?
1) battle!
2) Hot
3) green
4) swamping.
5) jump up.
6) undulate?
7) is.?
Which of the following matches regexp /[a-zA-Z]*[^,]=/?
1) Butt=
2) BotHEr,=
3) Ample
4) FIdDlE7h=
5) Brittle =
6) Other.=
Which of the following matches regexp /[a-z][\.\?!]\s+[A-Z]/?
(\s matches any space character)
1) A. B
2) c! d
3) e f
4) g. H
5) i? J
6) k L
Which of the following matches regexp /(very )+(fat )?(tall|ugly) man/?
1) very fat man
2) fat tall man
3) very very fat ugly man
4) very very very tall man
Which of the following matches regexp /<[^>]+>/?
1) <an xml tag>
2) <opentag> <closetag>
3) </closetag>
4) <>
5) <with attribute=”77”>
Write a regexp to identify dates of the form dd/mm/yyyy.
I expect dd to range from 1 to 31, and mm to range from 1 to 12, and I expect yyyy to not be 0000 (the Gregorian calendar predates this; see Year 0 and the invention of 0).
However, I do not expect you to cross-reference mm against dd or to restrict yyyy, so that e.g. 31/02/0231 is fine.
Write a regexp to identify dates of the form dd/mm/yyyy or dd.mm.yyyy, but not using mixed separators such as dd/mm.yyyy.
(Unmarked) Explain whether a regexp can identify correct bracketing, as in ((a)) but not (((a).
(Unmarked) Explain the relevance of the regexp /Whiske?y/
(Unmarked) Write a regexp for the set of even numbers (base 10; so the alphabet is [0-9]).

Back to F29LP

Question II: Grammars

Write a regular grammar to generate the language determined by the regexp /a*b*/
Write a regular grammar to generate the language determined by the regexp /(ab)*/
Write a regular grammar to generate the language matched by /Whiske?y/
Write a regular grammar to generate decimal numbers; the relevant regexp is /[1-9][0-9]*(\.[0-9]*[1-9])?/
Give a context free grammar for the language L = { aⁿ bⁿ | n ∈ ℕ}.
Give a context free grammar for the set of properly bracketed sentences over alphabet { 0 , ( , ) } (so 0 and ((0)) are fine, and 00 and 0) are not fine).
Write a context free grammar to generate possibly bracketed expressions of arithmetic with + and * and single digit numbers. So 0 and (0+9) are fine, and (0+)1 and 12 are not fine.
Give a grammar for palindromes over the alphabet { a , b }.
A parity-sequence is a sequence consisting of 0s and 1s that has an even number of ones. Give a grammar for parity-sequences.
Write a grammar for the set of numbers divisible by 4 (base 10; so the alphabet is [0-9]). You might like to read this page on divisibility testing, first.
(Unmarked) Write a grammar for the set of numbers divisible by 3 (base 10; so the alphabet is [0-9]).
(Unmarked) Write a grammar for the set of numbers divisible by 11 (base 10; so the alphabet is [0-9]).

Back to F29LP

Question III: More on grammars

State which of the following production rules are left-regular, right-regular, left-recursive, right-recursive, context-free (or more than one, or none, of these):
1. $\mbox{Thsi} \longrightarrow \mbox{This}\ $ (a rewrite auto-applied by Microsoft Word).
2. $\mbox{Sentence} \longrightarrow \mbox{Subject Verb Object}$. (Here Sentence, Subject, Verb, and Object are non-terminal symbols.)
3. $X \longrightarrow Xa$.
4. $X \longrightarrow XaX$.
What is the object language generated by $X \longrightarrow Xa$ (see lecture 2)?
Construct context-free grammars that generate the following languages:
1. $(ab|ba)^*$,
2. $\{(ab)^na^n\ |\ n\geq 1\}$,
3. $\{w\in\{a,b\}^*\ |\ \mbox{ $w$ is a palindrome }\}$,
4. $\{w\in\{a,b\}^*\ |\ \mbox{ $w$ contains exactly two $b$s and any number of $a$s }\}$,
5. $\{a^nb^m\ |\ 0\leq n\leq m\leq 2n \}$.
(Unmarked) Consider the grammar $G=(\{S,A,B\}, \{a,b\}, P, S)$ with productions
$$
\begin{array}{lcl}
S & \longrightarrow & S{}A{}B\ |\ \varepsilon\\
A & \longrightarrow & aA\ |\ \varepsilon\\
B & \longrightarrow & Bb\ |\ \varepsilon
\end{array}
$$
1. Give a leftmost derivation for $aababba$.
2. Draw the derivation tree corresponding to your derivation.
State with proof whether the following grammars are ambiguous or unambiguous:
1. $G=(\{S\}, \{a,b\}, P, S)$ with productions $S \longrightarrow aSa\ |\ aSbSa\ |\ \varepsilon$.
2. $G=(\{S\}, \{a,b\}, P, S)$ with productions $S \longrightarrow aaSb\ |\ abSbS\ |\ \varepsilon$.
Rewrite the following grammar to eliminate left-recursion:
$$
exp \longrightarrow exp + term \mid exp\ -\ term \mid term .
$$
Write a grammar to parse arithmetic expressions (with $+$ and $\times$) on integers (such as $0$, $42$, $-1$). This is a little harder than it first sounds because you will need to write a grammar to generate correctly-formatted positive and negative numbers; a grammar that generates $-01$ is unacceptable. You may use dots notation to indicate obvious replication of rules, as in “$D \longrightarrow 0 \mid \dots \mid 9$”, without comment.
Write two distinct parse trees for $2+3*4$ and explain in intuitive terms the significance of the two different parsings to their denotation.

Back to F29LP

Question IV: DFAs and NFAs

By writing a regular expression or a grammar, describe the language accepted by the DFA
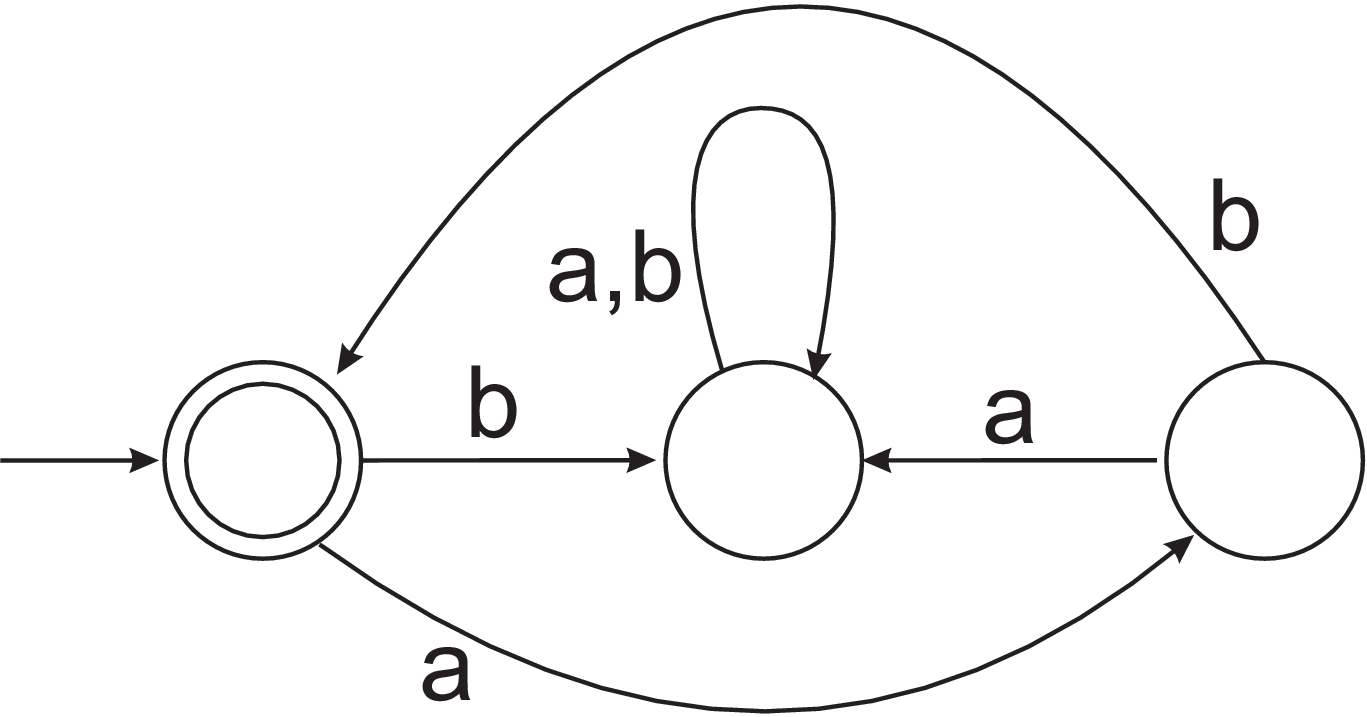
By writing a regular expression or a grammar, describe the language accepted by the DFA
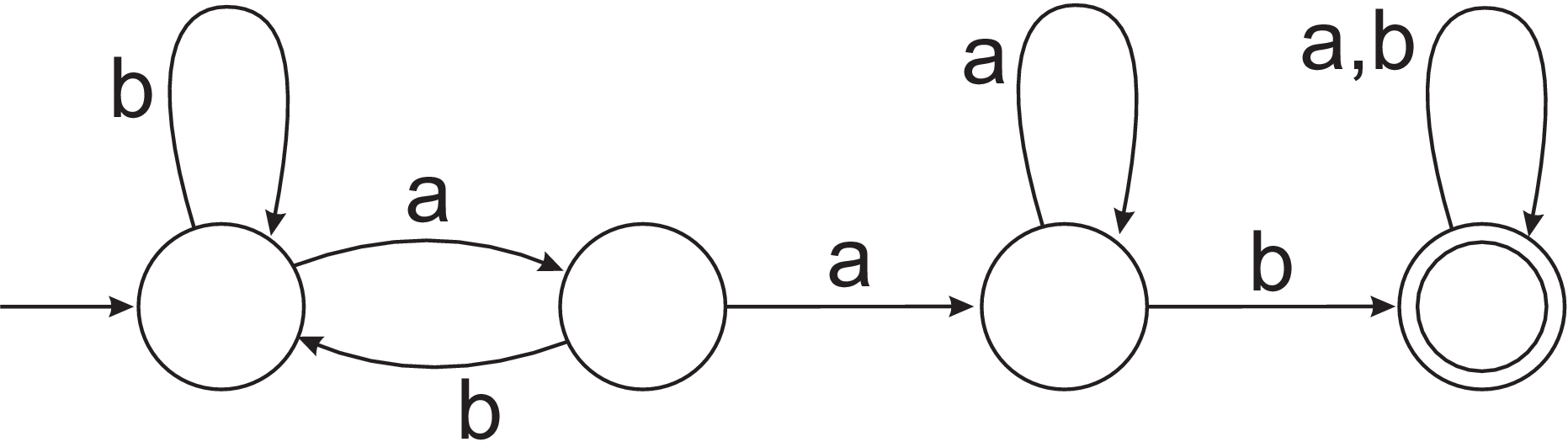
Construct NFAs (possibly with $\epsilon$-moves) to recognise the languages on alphabet {a,b} such that:
1. $L=\{w\in\{a,b\}^*\ |\ \mbox{ $w$ contains at most two $a$’s }\}$
2. $L=\{w\in\{a,b\}^*\ |\ \mbox{ $w$ contains an even number of occurrences of $ab$ as a subword }\}$
3. $L=\{w\in\{a,b\}^*\ |\ \mbox{ the first and the last letter of $w$ are identical }\}$
By writing a regular expression or a grammar, describe the language accepted by the NFA
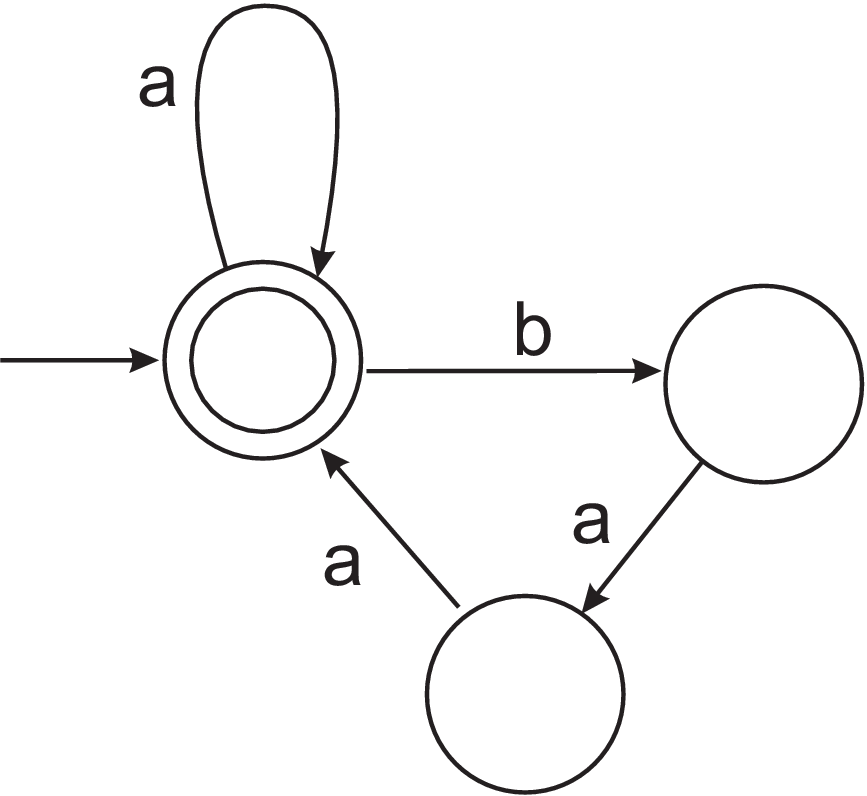
By writing a regular expression or a grammar, describe the language accepted by the NFA
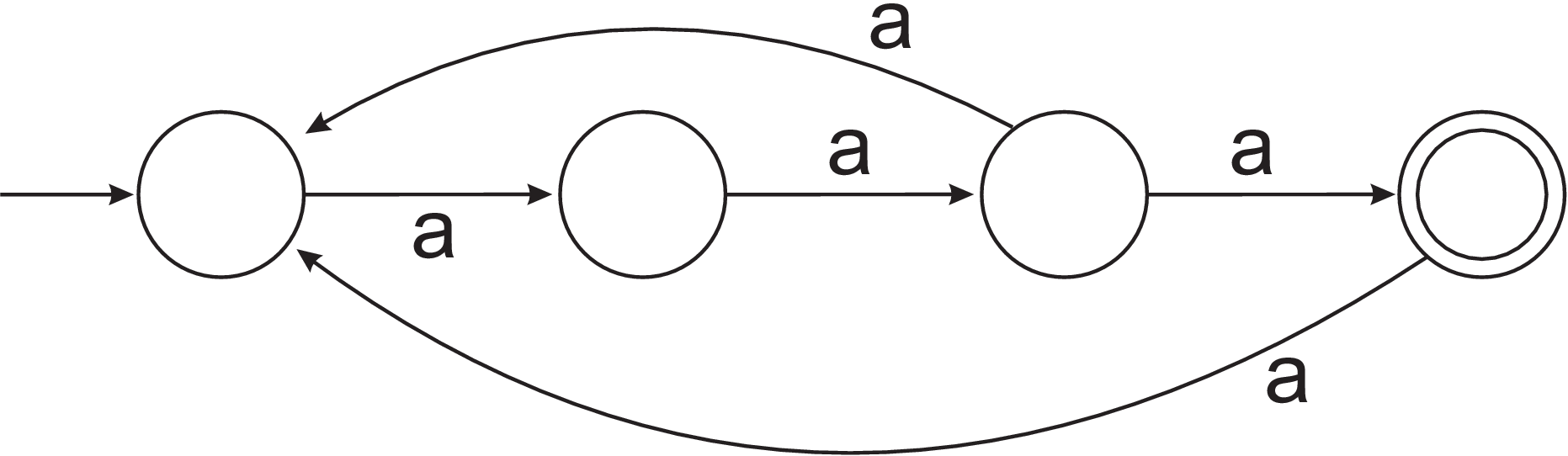
(Unmarked) Use the powerset construction (see lecture 5) to construct a DFA that recognises the same language as the following NFA:
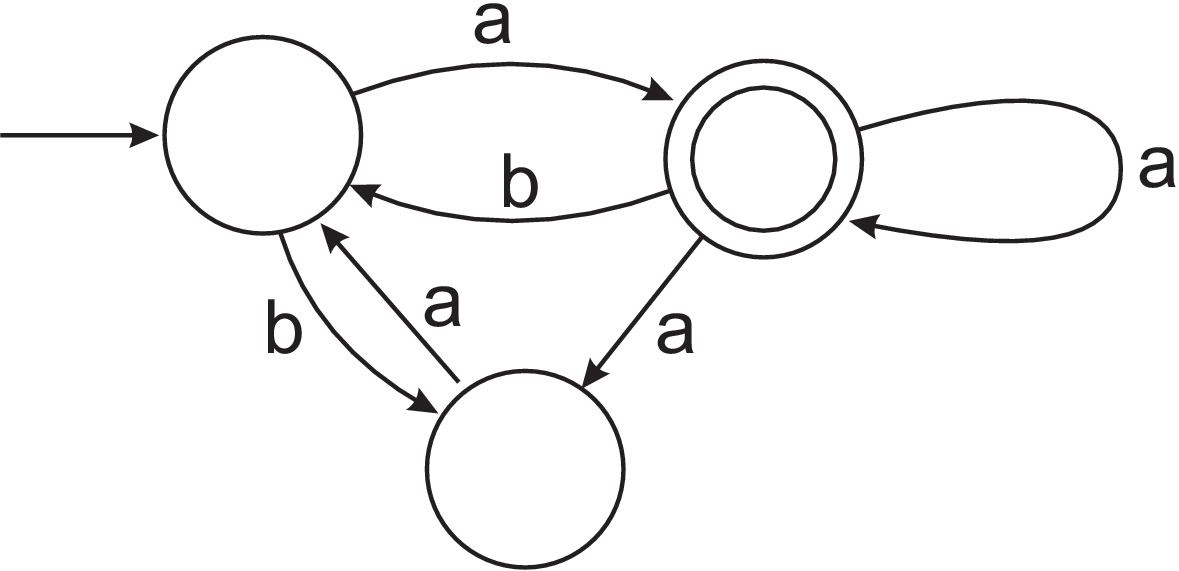
(Hard) Let $L$ be the language recognised by the NFA
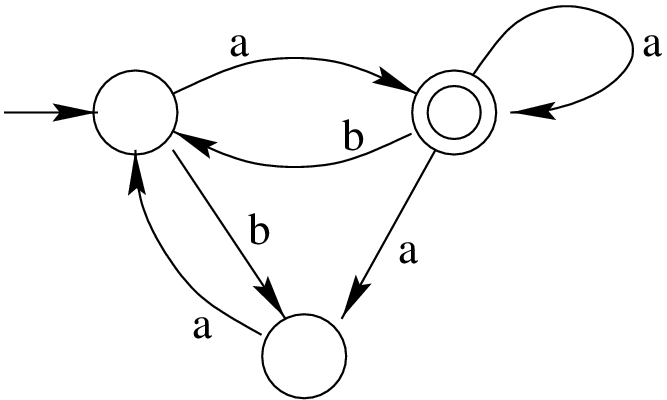
1. Construct a context-free grammar $G$ that generates language $L$.
2. State with proof whether $G$ is ambiguous or unambiguous.
(Unmarked) Let $G=(\{S,A,B\},\{a,b\},P,S)$ be the context-free grammar with productions
$$
\begin{array}{lcl}
S & \longrightarrow & aAbS\ |\ bBaS\ |\ \varepsilon,\\
A & \longrightarrow & aAbA\ |\ \varepsilon,\\
B & \longrightarrow & bBaB\ |\ \varepsilon.
\end{array}
$$
Give a short and intuitive English description of the language determined by $G$ (such a description does exist).

Back to F29LP

Question V: PDAs

In the questions below, assume the alphabet is $\{a,b\}$. Your answer must state the acceptance mode used.

Describe a pushdown automaton that recognises $\{a^m b^n a^m \mid m,n\geq 0 \}$.
Assume $m,n\geq 0$. Describe a DFA that recognises $\{a^m b^n a^m \}$.
Explain why this question is different from the previous question.
Describe a pushdown automaton that recognises $\{a^m b^{2n}\mid m,n\geq 0 \}$.
Describe a pushdown automaton that recognises $\{a^m b^n\mid m> n > 0 \}$.
Describe a pushdown automaton that recognises $\{ w \mid {\#{}_a} w={\#{}_b} w \}$,
where $\#{}_a w$ is the number of $a$s appearing in $w$ and $\#{}_b w$ is the number of $b$s appearing in $w$.
Describe a pushdown automaton that recognises $\{ w \mid \#{}_a w=2\#{}_b w \}$.
Describe a pushdown automaton that recognises $\{ w \mid \#{}_a w\neq \#{}_b w \}$.

Back to F29LP

Some exercises based on these notes.

Questions

Question I: regexps

Question II: Grammars

Question III: More on grammars

Question IV: DFAs and NFAs

Question V: PDAs