The activity model [Lones and Tyrrell, 2001c,Lones and Tyrrell, 2001b,Lones and Tyrrell, 2001a,Lones and Tyrrell, 2002a] is an earlier model of implicit context which predates the functionality model described in Chapter 8.
For the activity model, the shape of a component is its activity and the activity of a component is an instance of a function; not the function itself. This allows there to be multiple identifiable instances of a function, each recognised as a separate activity. Since shape is defined upon activity, so too are binding sites. Moreover, each component which receives input has a binding specificity defined for every outputting activity (input terminals and function instances) present within the program representation. An activity model program representation can be visualised as a fully-connected weighted network where the weight of a particular edge (the strength of a particular binding specificity) defines a relative preference for this edge being realised as a connection within the program. This idea is depicted in figure A.1. Evolution and program development proceed in the same manner as enzyme GP with the functionality model. Program representations are recombined using a uniform crossover operator. More details about the implementation of the activity model can be found in Lones and Tyrrell [2001c].
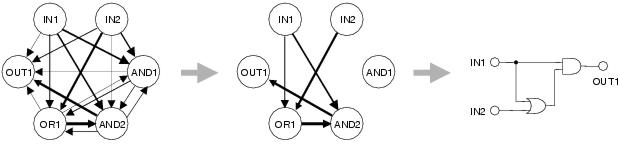
Figure A.1: Visualising the activity model. Shape is equivalent to activity. Connections show the specificity of one activity for input from another. Specificity strengths are shown by line weight. During development, the strongest specificities are realised as connections (within the bounds of the non-recurrency constraint).
| Population | Average (generations) | Success rate | Computational effort |
| 196 | 69 | 35% | 213,248 |
| 324 | 70 | 55% | 252,720 |
| 400 | 56 | 60% | 179,200 |
Table A.1: Performance of activity model upon two-bit multiplier problem.
Performance metrics for activity model enzyme GP upon the two-bit multiplier problem are listed in Table A for various population sizes. More detailed performance analysis, and comparison with the functionality model, can be found in Lones and Tyrrell [2002a]. Figure A.2 shows an example of a full adder being evolved with activity model enzyme GP. Note that whilst the behaviour of recombination is quite disruptive, recombination events still appear to play a significant role during evolution.
Programs evolved by the activity model are fixed-length and contain only pre-defined instances of components. Concern that the activity model contains excessive redundancy [Lones and Tyrrell, 2001c] and that it can not easily be extended to support variable-length solutions lead to the development of the functionality model.
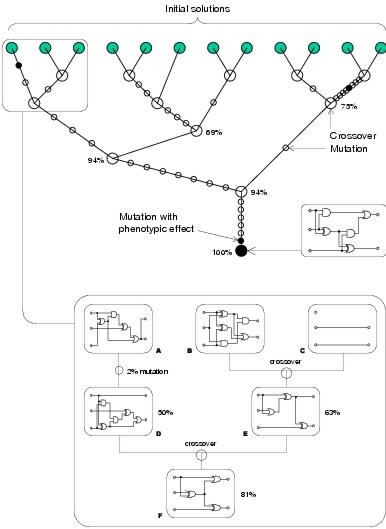
Figure A.2: Evolution of a full adder with the activity model. Both crossover and mutation are used to evolve an optimal solution. Most mutations are neutral. Note the neutral walk that leads to the optimum after the final recombination.