Reliable Massively Parallel Symbolic Computing: Fault Tolerance for a Distributed Haskell
The PhD thesis is available for download
- A compiled PDF here
- Thesis source: org-mode thesis, images, plot generation R scripts and results on GitHub here.
- Haskell implementation of HdpH-RS on GitHub here.
- Summarised in: Transparent Fault Tolerance for Scalable Functional Computation in the Journal of Functional Programming details.
- Presentation on the PhD research at: EPFL in Lausanne, Switzerland, July 2016 slides, details.
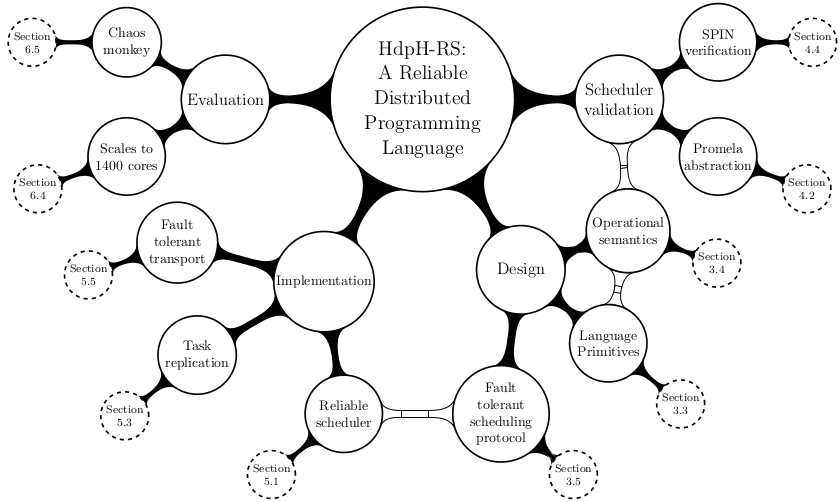
Chapter Titles
- Introduction
- Related Work
- Designing a Fault Tolerant Programming Language for Distributed Memory Scheduling
- The Validation of Reliable Distributed Scheduling for HdpH-RS
- Implementing a Fault Tolerant Programming Language and Reliable Scheduler
- Fault Tolerant Programming & Reliable Scheduling Evaluation
- Conclusion
Abstract
As the number of cores in manycore systems grows exponentially, the number of failures is also predicted to grow exponentially. Hence massively parallel computations must be able to tolerate faults. Moreover new approaches to language design and system architecture are needed to address the resilience of massively parallel heterogeneous architectures.
Symbolic computation has underpinned key advances in Mathematics and Computer Science, for example in number theory, cryptography, and coding theory. Computer algebra software systems facilitate symbolic mathematics. Developing these at scale has its own distinctive set of challenges, as symbolic algorithms tend to employ complex irregular data and control structures. SymGridParII is a middleware for parallel symbolic computing on massively parallel High Performance Computing platforms. A key element of SymGridParII is a domain specific language (DSL) called Haskell Distributed Parallel Haskell (HdpH). It is explicitly designed for scalable distributed-memory parallelism, and employs work stealing to load balance dynamically generated irregular task sizes.
To investigate providing scalable fault tolerant symbolic computation we design, implement and evaluate a reliable version of HdpH, HdpH-RS. Its reliable scheduler detects and handles faults, using task replication as a key recovery strategy. The scheduler supports load balancing with a fault tolerant work stealing protocol. The reliable scheduler is invoked with two fault tolerance primitives for implicit and explicit work placement, and 10 fault tolerant parallel skeletons that encapsulate common parallel programming patterns. The user is oblivious to many failures, they are instead handled by the scheduler.
An operational semantics describes small-step reductions on states. A simple abstract machine for scheduling transitions and task evaluation is presented. It defines the semantics of supervised futures, and the transition rules for recovering tasks in the presence of failure. The transition rules are demonstrated with a fault-free execution, and three executions that recover from faults.
The fault tolerant work stealing has been abstracted in to a Promela model. The SPIN model checker is used to exhaustively search the intersection of states in this automaton to validate a key resiliency property of the protocol. It asserts that an initially empty supervised future on the supervisor node will eventually be full in the presence of all possible combinations of failures.
The performance of HdpH-RS is measured using five benchmarks. Supervised scheduling achieves a speedup of 757 with explicit task placement and 340 with lazy work stealing when executing Summatory Liouville up to 1400 cores of a HPC architecture. Moreover, supervision overheads are consistently low scaling up to 1400 cores. Low recovery overheads are observed in the presence of frequent failure when lazy on-demand work stealing is used. A Chaos Monkey mechanism has been developed for stress testing resiliency with random failure combinations. All unit tests pass in the presence of random failure, terminating with the expected results.
Bibtex Entries
The JFP Paper
This JFP paper is a 41 page summary of the PhD thesis.
@article{DBLP:journals/jfp/StewartMT16,
author = {Robert J. Stewart and
Patrick Maier and
Phil Trinder},
title = {Transparent fault tolerance for scalable functional computation},
journal = {J. Funct. Program.},
volume = {26},
year = {2016},
doi = {10.1017/S095679681600006X}
}
The PhD thesis
@phdthesis{Stewart13,
author = {Robert Stewart},
title = {{Reliable Massively Parallel Symbolic Computing: Fault Tolerance for a Distributed Haskell}},
school = {{Mathematical and Computer Sciences, Heriot-Watt University}},
address = {Edinburgh, Scotland},
year = {2013},
month = {November}
}