Deadlines
- The deadline for QI and QII is Thursday 31 January (end of the day).
- The deadline for QIII is Friday 8 February (end of the day).
- The deadline for QIV and QV is Friday 15 February (end of the day).
Submission is via pdf uploaded to the relevant TurnItIn assignments on Vision. I love Vision.
Note that these questions contribute to your final exam mark.
Question I: regexes
Notes on answering this question: In my experience the most convincing presentation for your answers is to cut-and-paste the text below, then just highlight the non-matching regexes in RED and the matching regexes in GREEN. So you end up with a pretty multicolour list of QandAs, and the marker just scans the page looking for the right pattern. You’re very welcome to write an English justification; this is not required by the question but may help the marker to understand your thinking and so give you feedback.
In the questions below, “matches” refers to whole-string matching (and not to matching a substring).
- Which of the following matches regex /
abababa/?
1)abababa
2)aaba
3)aabbaa
4)aba
5)aabababa - Which of the following matches regex /
ab+c?/?
1)abc
2)ac
3)abbb
4)bbc - Which of the following matches regex /
a.[bc]+/?
1)abc
2)abbbbbbbb
3)azc
4)abcbcbcbc
5)ac
6)asccbbbbcbcccc - Which of the following matches regex /
abc|xyz/?
1)abc
2)xyz
3)abc|xyz - Which of the following matches regex /
[a-z]+[\.\?!]/?
1)battle!
2)Hot
3)green
4)swamping.
5)jump up.
6)undulate?
7)is.? - Which of the following matches regex /
[a-zA-Z]*[^,]=/?
1)Butt=
2)BotHEr,=
3)Ample
4)FIdDlE7h=
5)Brittle =
6)Other.= - Which of the following matches regex /
[a-z][\.\?!]\s+[A-Z]/?
(\s matches any space character)
1)A. B
2)c! d
3)e f
4)g. H
5)i? J
6)k L - Which of the following matches regex /
(very )+(fat )?(tall|ugly) man/?
1)very fat man
2)fat tall man
3)very very fat ugly man
4)very very very tall man - Which of the following matches regex /
<[^>]+>/?
1)<an xml tag>
2)<opentag> <closetag>
3)</closetag>
4)<>
5)<with attribute=”77”> - Write a regex to identify dates of the form dd/mm/yyyy.
I expect dd to range from 01 to 31, and mm to range from 01 to 12, and I expect yyyy to range from 0001 to 9999 and in particular to not be 0000 (the Gregorian calendar predates this; see Year 0 and the invention of 0).
However, I do not expect you to cross-reference mm against dd or to restrict yyyy, so that e.g. 31/02/0231 is fine.
Do not use backreferences or negative lookahead (so if your answer contains?!, then it’s not admissible for this question). - Write a regex to identify dates of the form dd/mm/yyyy or dd.mm.yyyy, but not using mixed separators such as dd/mm.yyyy.
You may use backreferences, negative lookahead, and other fancy tricks, if convenient. - (Unmarked) Explain whether a regex can identify correct bracketing, as in
((a))but not(((a). - (Unmarked) Explain the relevance of the regex /
Whiske?y/ - Write a regex for the set of even numbers without leading zeroes (base 10; so the alphabet is
[0-9]). Note that 0 and 2 and 10 and 20 are even numbers without leading zeroes, and 00 and 02 and 1 and 01 are not even numbers without leading zeroes. Check that your regex accepts 100 and 10012.
Question II: Grammars
Notes on answering this question:
- Pay attention to what kind of grammer I ask for (regular, or context free, or some other type).
- For instance: if I ask for a regular grammar and you give me some other kind of grammer, then you may lose marks!
- In particular, if your regular grammar contains a rule of the form $S \longrightarrow ab\gamma$ or $S \longrightarrow D$ or $S \longrightarrow \varepsilon D$, then this is not a regular grammar and your answer contains an error.
- Always clearly specify the start symbol.
- The alphabet (set of tokens) of a language cannot contain ε. ε is the empty string, that is, an absence of tokens. If your answer contains something of the form T={ε,…} (where T is supposed to be a set of tokens for your language) — then your answer is probably wrong and you’re probably losing marks.
Some of you have not met sets notation before, so here’s a quick tutorial:
- The language determined by the regex /a*/ is { aⁿ | n ∈ ℕ} or equivalently { aⁿ | n ∈ {0,1,2,…} } or equivalently { aⁿ | n ≥ 0 }.
- The language determined by the regex /(a|b)?/ is { a, b, ε }.
- The language determined by the regex /a+b+/ is { aᵐbⁿ | m,n ≥ 1 } or equivalently { aᵐbⁿ | m ≥ 1, n ≥ 1 } or equivalently { aᵐbⁿ | m,n ∈ {1,2,3,…} }.
- The language determined by the English description “any nonzero digit” is { 1, 2, 3, 4, 5, 6, 7, 8, 9} or equivalently { 1, 2, … , 9} or equivalently { n | 9 ≥ n ≥ 1 } or equivalently { n | 0 < n ≤ 9 }.
Now on to the questions:
- Write the language determined by the regex /
a*b*/ - Write a regular grammar to generate the language determined by the regex /
a*b*/ - Write the language determined by the regex /
(ab)*/ - Write a regular grammar to generate the language determined by the regex /
(ab)*/ - Write the language determined by /
Whiske?y/. The alphabet is {W,h,i,s,k,e,y} (W is a terminal symbol here). - Write a regular grammar to generate the language matched by /
Whiske?y/ - Write a regular grammar to generate decimal numbers; the relevant regex is /
[1-9][0-9]*(\.[0-9]*[1-9])?/.
You may find it useful to use notation resembling D ::= 0 | 1 | … | 9 to denote an evident set of ten production rules. - Give a context free grammar for the language L = { aⁿ bⁿ | n ∈ ℕ}.
- Give a context free grammar for the set of properly bracketed sentences over alphabet {
0,(,)}. So0and((0))are fine, and00and0)are not fine. - Write a context free grammar to generate possibly bracketed expressions of arithmetic with + and * and single digit numbers. So
0and(0)and0+1+2and(0+9)are fine, and(0+)1and12are not fine. - Give a grammar for palindromes over the alphabet {
a,b}. - A parity-sequence is a sequence consisting of 0s and 1s that has an even number of ones. Give a grammar for parity-sequences.
- Write a grammar for the set of numbers divisible by 4 (base 10; so the alphabet is
[0-9]). You might like to read this page on divisibility testing, first. You may use dots notation to represent an evident sequence, as in for example the sequence $Z3,Z6,Z9,\dots,Z999$ to mean “Z followed by some number divisible by three and strictly between 0 and 1000”. - Write a grammar for the set of numbers divisible by 3 (base 10; so the alphabet is
[0-9]). So for example0,003, and120should be in your language, and1,2, and5should not. - (Unmarked) Write a grammar for the set of numbers divisible by 11 (base 10; so the alphabet is
[0-9]).
Question III: More on grammars
- State which of the following production rules are left-regular, right-regular, left-recursive, right-recursive, context-free (or more than one, or none, of these):
- $\mbox{Thsi} \longrightarrow \mbox{This}\ $ (a rewrite auto-applied by Microsoft Word).
- \(\mbox{Sentence} \longrightarrow \mbox{Subject Verb Object}\). (Here Sentence, Subject, Verb, and Object are non-terminal symbols.)
- $X \longrightarrow Xa$.
- $X \longrightarrow XaX$.
- What is the object language generated by $X \longrightarrow Xa$ (see lecture 2)? Explain your answer.
- Construct context-free grammars that generate the following languages:
- $(ab|ba)^*$,
- $\{(ab)^na^n\ |\ n\geq 1\}$,
- $\{w\in\{a,b\}^*\ |\ \mbox{ $w$ is a palindrome }\}$,
- $\{w\in\{a,b\}^*\ |\ \mbox{ $w$ contains exactly two $b$s and any number of $a$s }\}$,
- $\{a^nb^m\ |\ 0\leq n\leq m\leq 2n \}$.
- Consider the grammar $G=(\{S,A,B\}, \{a,b\}, P, S)$ with productions
$$
\begin{array}{lcl}
S & \longrightarrow & S{}A{}B\ |\ \varepsilon\\
A & \longrightarrow & aA\ |\ \varepsilon\\
B & \longrightarrow & Bb\ |\ \varepsilon
\end{array}
$$- Give a leftmost derivation for $aababba$.
- Draw the derivation tree corresponding to your derivation.
- State with proof whether the following grammars are ambiguous or unambiguous:
- $G=(\{S\}, \{a,b\}, P, S)$ with productions $S \longrightarrow aSa\ |\ aSbSa\ |\ \varepsilon$.
- $G=(\{S\}, \{a,b\}, P, S)$ with productions $S \longrightarrow aaSb\ |\ abSbS\ |\ \varepsilon$.
- Rewrite the following grammar to eliminate left-recursion:
$$
exp \longrightarrow exp + term \mid exp\ -\ term \mid term .
$$ - Write a grammar to parse arithmetic expressions (with $+$ and $\times$) on integers (such as $0$, $42$, $-1$). This is a little harder than it first sounds because you will need to write a grammar to generate correctly-formatted positive and negative numbers; a grammar that generates $-01$ is unacceptable. You may use dots notation to indicate obvious replication of rules, as in “$D \longrightarrow 0 \mid \dots \mid 9$”, without comment.
(Note that a parser is not an evaluator. This question is not asking you to write an evaluator. Also note that the grammar only needs to be unambiguous if the question asks you to provide an unambiguous grammar.) - Write two distinct parse trees for $2+3*4$ and explain in intuitive terms the significance of the two different parsings to their denotation.
Question IV: DFAs and NFAs
You may find draw.io useful for drawing automata. If you know of a similar and better tool, please let me know.
- By writing a regular expression or a grammar, describe the language accepted by the DFA
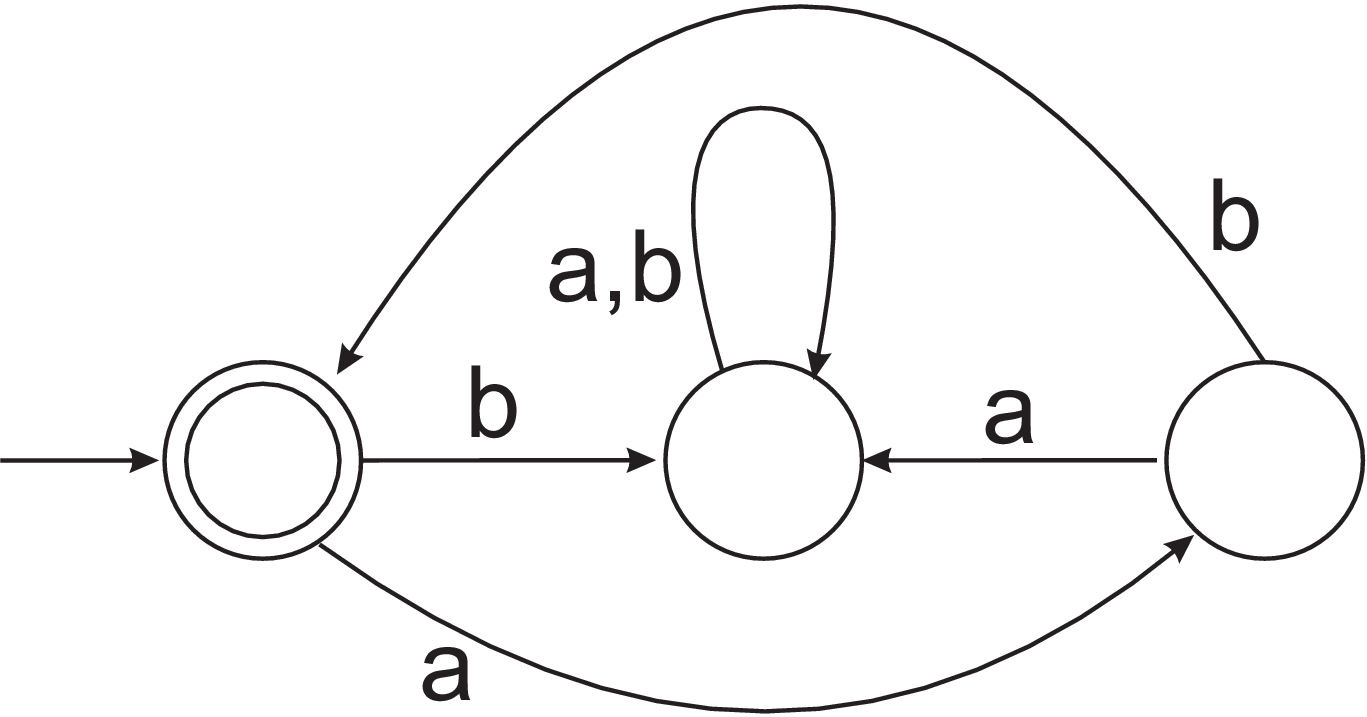
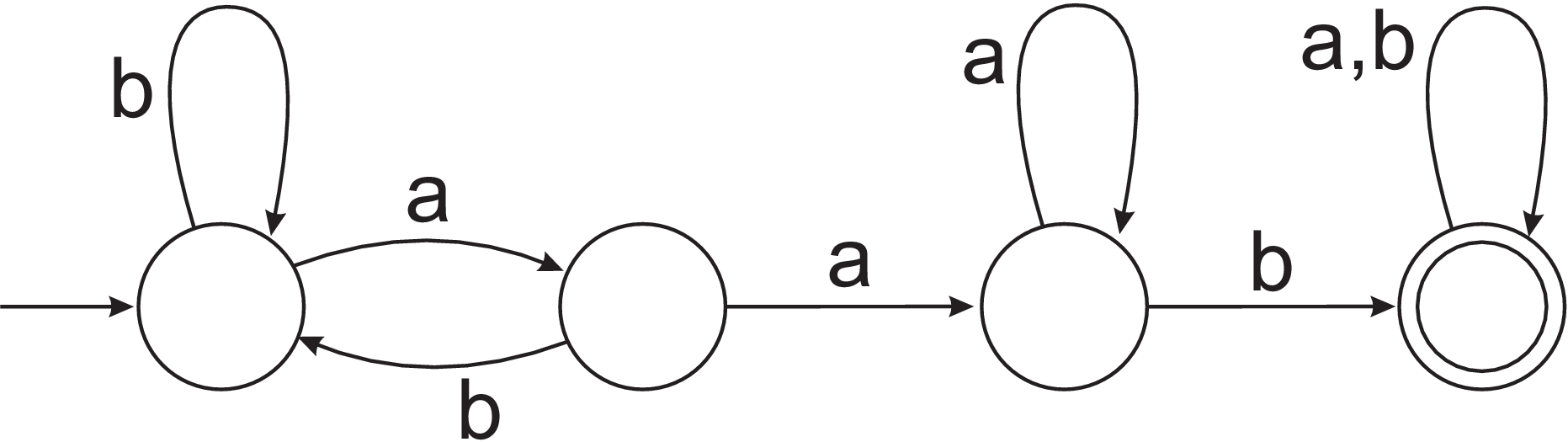
- By writing a regular expression or a grammar, describe the language accepted by the DFA
- Construct NFAs (possibly with $\epsilon$-moves) to recognise the languages on alphabet {a,b} such that:
- $L=\{w\in\{a,b\}^*\ |\ \mbox{ $w$ contains at most two $a$s }\}$ So $\epsilon$ and $aa$ and $bbbbabba$ are in $L$ and $aaa$ is not.
- $L=\{w\in\{a,b\}^*\ |\ \mbox{ $w$ contains an even number of occurrences of $ab$ as a subword }\}$ So $\epsilon$ and $a$ and $b$ and $abab$ and $abaaba$ and $baaabab$ are in $L$, but $ab$ and $ababab$ and $abaabab$ are not.
- $L=\{w\in\{a,b\}^*\ |\ \mbox{ the first and the last letter of $w$ are identical }\}$
- By writing a regular expression or a grammar, describe the language accepted by the NFA
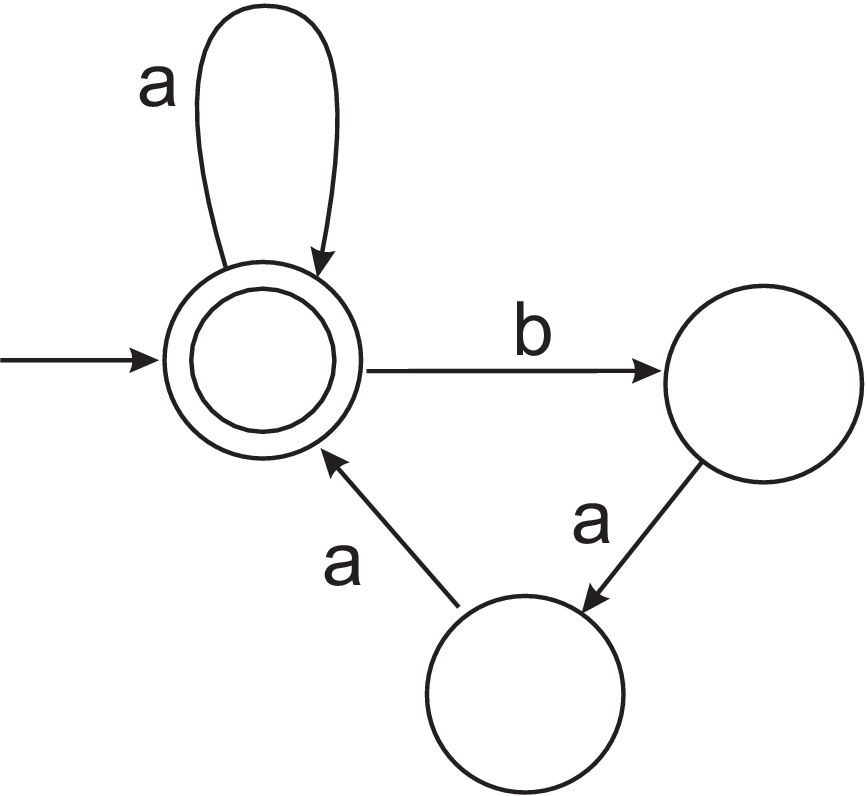
- By writing a regular expression or a grammar, describe the language accepted by the NFA
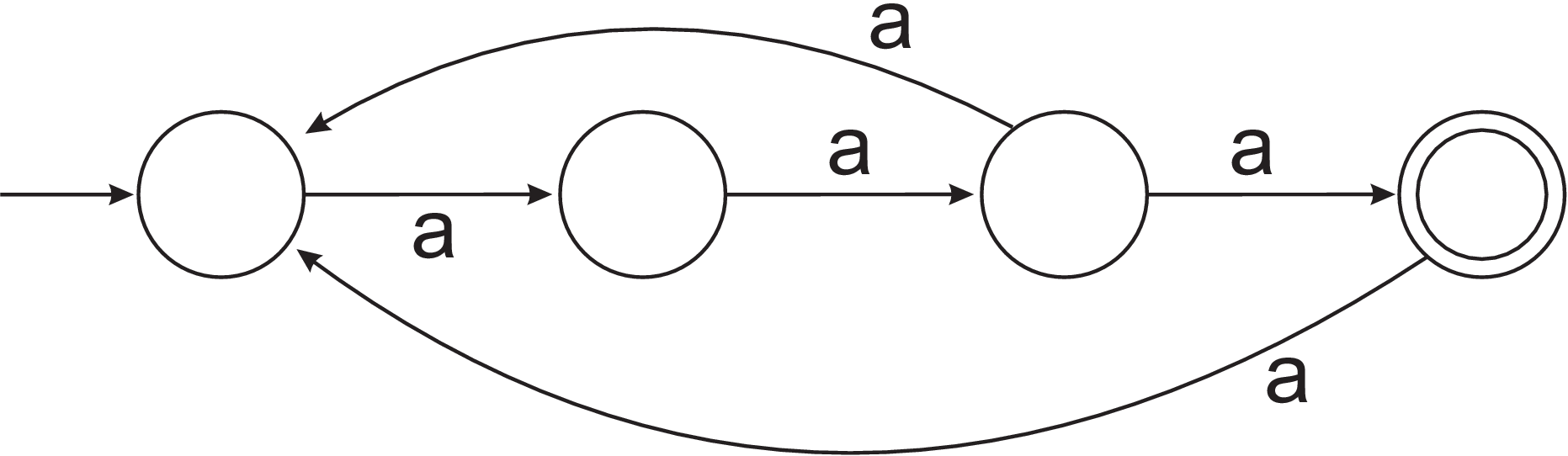
- (Unmarked) Use the powerset construction (see lecture 5) to construct a DFA that recognises the same language as the following NFA:
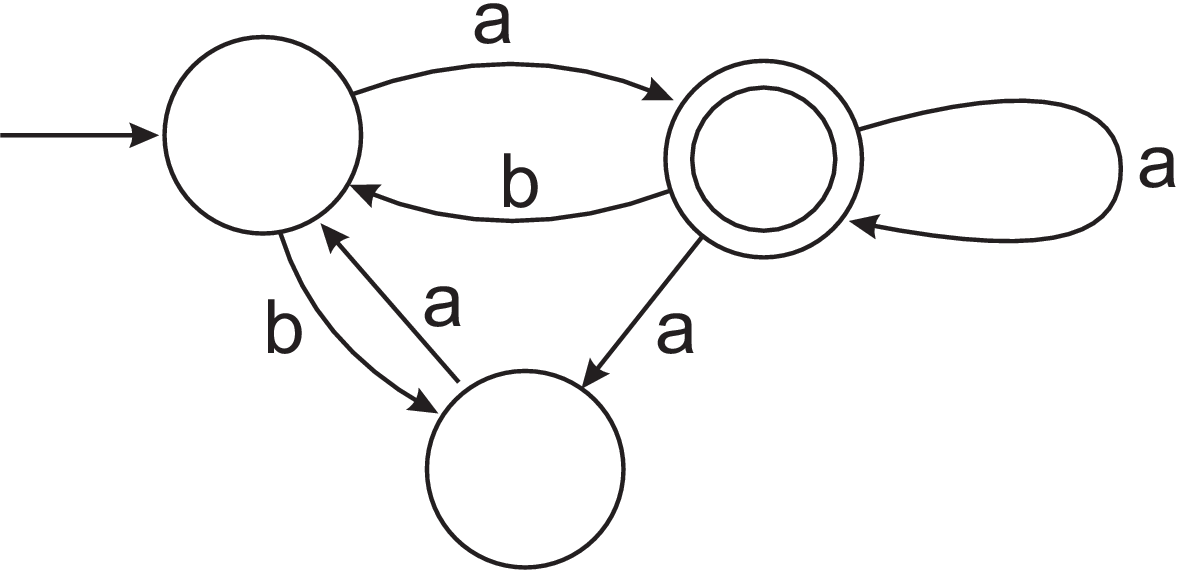
- (Hard) Let $L$ be the language recognised by the NFA
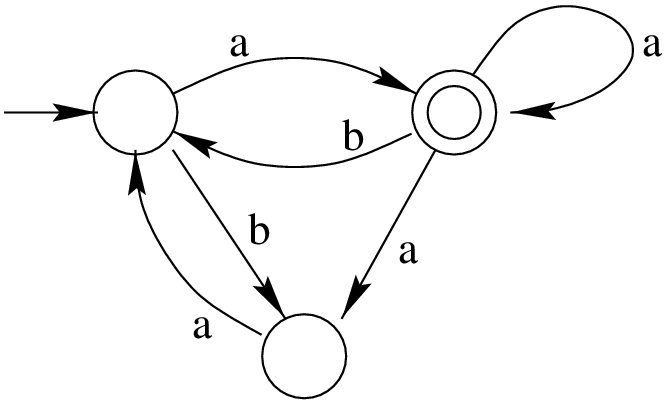
- Construct a context-free grammar $G$ that generates language $L$ (a regular grammar is also fine, since every regular grammar is context-free).
- State with proof whether $G$ is ambiguous or unambiguous.
- (Unmarked) Let $G=(\{S,A,B\},\{a,b\},P,S)$ be the context-free grammar with productions
$$
\begin{array}{lcl}
S & \longrightarrow & aAbS\ |\ bBaS\ |\ \varepsilon,\\
A & \longrightarrow & aAbA\ |\ \varepsilon,\\
B & \longrightarrow & bBaB\ |\ \varepsilon.
\end{array}
$$
Give a short and intuitive English description of the language determined by $G$ (such a description does exist).
Question V: PDAs
In the questions below, assume the alphabet is $\{a,b\}$. Your answer must state the acceptance mode used. In the questions below, the word describe means draw a precise picture of in the style I used in lectures or in the style of this webpage or this pdf, or just search the Internet for how to draw a PDA.
- Describe a pushdown automaton that recognises \(\{a^m b^n a^m \mid m,n\geq 0 \}\).
- Assume \(m,n\geq 0\). Describe a DFA that recognises \(\{a^m b^n a^m \}\).
Explain why this question is different from the previous question. - Describe a pushdown automaton that recognises \(\{a^m b^{2n}\mid m,n\geq 0 \}\).
- Describe a pushdown automaton that recognises \(\{a^m b^n\mid m> n > 0 \}\).
- Describe a pushdown automaton that recognises \(\{ w \mid {\#{}_a} w={\#{}_b} w \}\),
where \(\#{}_a w\) is the number of $a$s appearing in $w$ and \(\#{}_b w\) is the number of $b$s appearing in $w$. - Describe a pushdown automaton that recognises \(\{ w \mid \#{}_a w=2\#{}_b w \}\).
- Describe a pushdown automaton that recognises \(\{ w \mid \#{}_a w\neq \#{}_b w \}\).
Some exercises based on these notes.