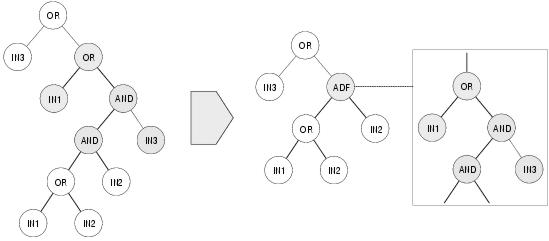
Figure 7.1: Introducing a capacity for pleiotropy using Koza's branch creation operator.
This chapter is a review of research aimed at improving the evolvability of the artefacts which are evolved by evolutionary computation techniques. In particular, it attempts to address those issues which are of special relevance to genetic programming. Where appropriate, this includes research done in other fields of evolutionary computation.
In Chapter 1, evolutionary change was described as the result of sources of variation acting upon the representation of an entity. From this it follows that the nature of evolutionary change might be improved by either (i) improving the ability of variation to enact appropriate change; or (ii) improving the ability of the representation to accept appropriate change. Both of these are valid. Nevertheless, in this thesis, emphasis is clearly placed upon the second of these approaches. This is for two reasons.
First, whilst variation mechanisms are an important part of biological evolution, their behaviours appear relatively simple when compared to the rich organisation, developmental mechanisms, and behavioural scope of biological representations. Even recombination, which is under evolutionary control, carries out a non-deterministic behaviour whose evolutionary effect is determined primarily by the response of the representation. In looking for biological guidance concerning evolvability it would seem, therefore, that more information could be gleaned by looking at biological representations rather than the sources of variation within biological evolution.
Secondly, it is common knowledge in computer science that if the same effect can be achieved by improving the way information is represented or by improving the way information is operated upon, better generality can be achieved by adapting the representation. For instance, if the information in a database is structured in a way that makes certain information difficult to manipulate, it would be considered better in the long run to improve the way the database is structured rather than improve the complexity of queries used to manipulate the information. Likewise, in the first instance it would seem better in the long run to change the way an evolving entity is represented rather than the way in which it is manipulated if both are capable of improving the way that it evolves.
Nevertheless, some interesting work has been done in adapting variation operators. This is briefly reviewed in the next section. The remaining sections of this chapter are concerned with existing approaches to improving the evolvability of representations. These are organised according to the manner in which they attempt to introduce evolvability: through pleiotropy, redundancy or removal of positional bias. In part this requires some familiarity with information from the previous chapter and from Chapter 5.
In the last chapter, the relative failure of sub-tree crossover in genetic programming was attributed to the unlikelihood of it carrying out meaningful recombinative behaviours. A number of researchers [Poli and Langdon, 1997,Langdon, 1999,Langdon, 2000b,Francone et al., 1999,Hansen, 2003a] have looked at the possibility of constraining the behaviour of GP crossover in order to prevent inappropriate behaviours. This has led to a range of homologous crossover operators which attempt to limit genetic exchange to regions of genetic homology. One-point crossover [Poli and Langdon, 1997,Poli and Langdon, 1998], which resembles GA one-point crossover, does this by identifying and using a crossover point which occurs in the same position within both parent parse trees. Uniform crossover [Poli and Langdon, 1998] models GA uniform crossover by identifying regions of common position and shape within both parents and uniformly recombining the nodes within these regions. However, neither of these operators lead to a significant increase in performance and both introduce a considerable processing overhead in identifying homologous regions. Size-fair crossover [Langdon, 1999] uses a different approach and only constrains sub-tree crossover to sub-trees of equal size, though again produces little increase in performance. More recently, Langdon [2000b] has extended this approach by using a formal definition of genetic distance based upon location and size to determine where crossover events may occur. This has produced more encouraging results, although requiring more computational overhead during crossover.
The only homologous recombination operator to produce a sizeable improvement in performance is Francone et al's sticky crossover which works on linear GP programs. Sticky crossover is a relatively simple homologous operator which limits recombination to groups of instructions with common offsets and common lengths. Francone et al. believe that sticky crossover leads to programs with better generality and higher robustness than standard linear GP programs. Hansen [2003a] shows that sticky crossover offers superior performance across a wide range of regression problems and that the resulting programs contain lower incidences of intronic code (see section 7.4.1 for a definition of intronic code). The relative failure and complexity of tree GP homologous crossover operators when compared to sticky crossover tends to suggest that the linear GP program representation is innately more amenable to meaningful recombination than the parse tree structure of standard GP.
Recall from section 5.1 that compartmentalisation is the limitation of interactions between different sub-systems. In the context of biological systems, it was suggested that compartmentalisation introduces de-constraint: allowing sub-systems to evolve independently. Nevertheless, it is also believed that pleiotropy - the sharing of genes between sub-systems; conceptually the opposite of compartmentalisation - plays an important role by way of reducing the need to re-evolve the same functionality in different sub-systems. Tree-structured GP representations, by default, confer complete compartmentalisation to the programs they represent: since every function and terminal instance is involved in exactly one sub-expression. However, given limited availability of time and space, many researchers believe there is virtue in introducing pleiotropy to GP systems: reducing the time requirement by preventing the need to re-discover functionality; and reducing the space requirement by preventing the need to store the same sub-expression at multiple locations in the same program. This section introduces two general approaches to introducing pleiotropy to GP: modularity and implicit reuse.
Much of the work on modularity in GP has been carried out by Koza . His earliest work took the form of a `define building block' operator which named subtrees and allowed them to be referenced elsewhere in the program as zero-argument functions [Koza, 1992]. Later, this idea was extended to the notion of automatically-defined functions (ADFs): argument-taking functions stored in trees which co-evolve with the main routine [Koza, 1994]. The architecture of the program - the number, argument-signatures, and hierarchical limits of these modules - has to be chosen before evolution begins, either by prospective analysis, which requires knowledge of problem-decomposition; over-specification, sufficient modules for any possible needs; affordable capacity, since more modules entail more processing; retrospective analysis, from feedback of previous runs; or by evolutionary selection, which uses an initial population seeded with many different architectures. Results reported in [Koza, 1992] and [Koza, 1994] suggest that use of ADFs can lead to a considerable decrease in the time required to solve certain problems. This is especially true for problems, like parity checkers, whose solutions require a high level of functional duplication. ADFs have also been shown to decrease the size of evolved solutions.
Nevertheless, from an evolutionary perspective, ADFs have distinct limitations. First, it is not possible for a program's architecture to evolve. This places a limit upon modularity and, if the initial architecture is not appropriate, may hinder evolution. Second, there is no obvious mechanism for introducing de-constraint. Change to an ADF will affect the behaviour of the program at each calling instance. Whilst this may sometimes be appropriate, sometimes it will not. For example, suppose an ADF is called from two different sub-trees in a program and, so far, the functionality of the ADF has been beneficial to the behaviour of both sub-trees. Now suppose that in order to progress further, the behaviour of the sub-trees must diverge. In this situation, pleiotropy between the two sub-trees in their shared use of the ADF is constraining further evolution since changes to the ADF which would benefit one sub-tree would not benefit the other. The only way of removing this constraint would be for the variation operators to replace at least one of the calls to the ADF with a copy of the code from the ADF: which would require a highly unlikely sequence of matings and crossovers.

Figure 7.1: Introducing a capacity for pleiotropy using Koza's branch creation operator.
To overcome these limitations, Koza [1995] proposed a collection of architecture altering operators inspired in part by the biological process of gene duplication. Gene duplication removes de-constraint by duplicating a pleiotropic gene, allowing the two versions to evolve in different directions. Koza's branch duplication operator does the same by duplicating ADFs. After duplication, some of the calls to the original ADF are randomly replaced by calls to the duplicate ADF. Koza calls this procedure case-splitting to reflect the fact that it can lead to functional specialisation: from one general ADF to multiple more specialised copies of the ADF. Functional specialisation can also be achieved through argument duplication: whereby extra arguments are presented to an ADF by duplicating existing arguments. Following argument duplication, references within the ADF to the existing parameter are updated randomly so that some of them now refer to the new duplicate parameter. Thereafter, the duplicated argument sub-trees below an ADF call will undergo separate evolution: another form of case splitting. Koza also describes operators which attempt to introduce pleiotropy. Branch creation transforms a randomly selected region of code into an ADF: replacing the code at its original position with an ADF function call and preserving the code below the removed code as arguments to the function call (see figure 7.1 for an example). Code elsewhere in the program may then call the ADF, thus introducing pleiotropy. Branch and argument deletion operators attempt to do the opposite to the duplication operators by generalising existing ADFs and arguments and reversing the move towards larger more specialised programs. However, without knowing what the code does, there is little chance that these operators will produce meaningful code, let alone a generalisation.
Other approaches to modularity in GP derive from an engineering viewpoint. In software engineering environments, modules are stored in libraries that are shared between programs. Over time new modules are added to libraries and existing modules are improved or possibly subsumed by new modules. The earliest example of a library approach in GP is Module Acquisition (MA) [Angeline, 1994]. In MA, a compress operator randomly selects blocks of code to place in a global library where they may be referenced by any member of the population. However, since there is no selection for modules with useful (or even any) functionality, MA's library often only succeeds in propagating poor or non-functional blocks of code from one program to another. A more successful library-based approach to GP modularity is Rosca and Ballard's Adaptive Representation through Learning (ARL) [Rosca and Ballard, 1996] (and to a lesser extent, the earlier Adaptive Representation [Rosca and Ballard, 1994]). Central to their approach is the idea that the use of subroutines reduces the size of the search space by forcing the evolutionary mechanism towards productive regions. By steadily increasing the level of complexity within elements of the representational language (i.e. building programs out of high-level functions rather than primitives), the search space can be divided and conquered. However, this requires that building blocks be of high quality, since high-level functionality depends upon low-level functionality [Rosca and Ballard, 1995]. ARL attempts to identify high-quality blocks of code using two criteria: differential fitness and block activation. Differential fitness is used to identify which programs to extract code segments from, and block activation is used to identify which code segments to extract. Differential fitness is a measure of how much fitter a solution is than its least fit parent. If a program has high differential fitness, then it is likely that it contains a new fit block of code which was not present in its parents. Within a program, some blocks of code are more active than others, and presumably more useful. The most active blocks from the most differentially-fit parents are called salient blocks, and these are the targets for re-use. Once programs with the highest differential fitnesses have been identified, salient blocks are detected by logging the frequency of activation of the root nodes of blocks. Before these are stored separately as modules, they are generalised by replacing random subsets of their terminals with variables, which are provided by arguments in function invocations. Once they are stored, they enter competition with other subroutines. Subroutines have utility value, the average fitness of all programs which have invoked the subroutine over a number of generations. Invocation is either direct, by programs, or indirect, by other subroutines. In the latter case, the lower-level subroutines receive a reward each time the higher-level subroutine is called, meaning that essential low-level routines have a good chance of survival. Subroutines with low utility value are periodically removed from storage, textually replacing each of their function invocations in calling programs.
Implicit reuse it an example of how a degree of reuse may be achieved purely through a change in representation. Unlike modularity, implicit reuse is not an intentional approach to reuse; but rather a natural by-product of representations which allow multiple references to a single sub-structure. The best examples of these are graphical representations where nodes can have more than one output connection. Obviously this is not possible with a tree representation, since by definition each node in a tree has exactly one parent node. Both Poli [1997], in the context of PDGP, and Miller and Thomson [2000], in the context of cartesian GP, describe a tendency for the evolutionary process to take advantage of implicit reuse. Given the absence of any variational pressure in this direction, this suggests that a certain degree of pleiotropy is beneficial to evolution: since those programs that exhibit pleiotropy have evidently out-competed programs with no pleiotropy.
There is considerable interest in the research community in the role that redundancy plays within the representations of evolutionary algorithms. This interest can be classified according to three themes: structural redundancy, coding redundancy (particularly the role of neutrality), and functional redundancy. The organisation of this section reflects these three themes.
In section 5.2.2 structural redundancy was defined as the occurrence of complexity higher than that required to fulfill a phenotypic task. Within biological systems, structural redundancy has been theorised as playing an important role in increasing the evolvability of biological components and structures: either by enabling gradual change or by shielding existing components from disruption by sources of variation. In evolutionary computation, most of the interest in structural redundancy has concentrated on the second of these roles: in particular, the role of non-coding components in providing protection against crossover.
Non-coding inter-genic regions within biological chromosomes are thought responsible for segregating genes and thereby making it more likely that crossover junctions will form between, rather than within, genes. Likewise, according to the exon shuffling hypothesis of gene evolution [Gilbert, 1978], inter-genic non-coding regions (introns) segregate the coding parts of genes, making them more likely to be re-arranged to form new genes rather than be disrupted by crossover events. Within the EC literature, non-coding components of evolving solutions are generally termed introns; even though in most cases EA introns correspond more closely to intra-genic non-coding regions than inter-genic regions.
Some of the earliest interest in introns in evolutionary algorithms came with the introduction of explicit introns into the candidate solution strings of genetic algorithms. Ordinarily, introns do not occur within the candidate solutions of canonical GAs; prompting a number of researchers [Levenick, 1991,Forrest and Mitchell, 1993,Wu and Lindsay, 1995,Wu and Lindsay, 1996a,Wu and Lindsay, 1996b] to suggest that introns within GAs could play similar beneficial roles to those which they are hypothesised to play within biological systems. Indeed, results by Levenick [1991] upon a simple model of a biological adaption problem showed that performance improved by a factor of ten when introns were introduced between pairs of genes. However, later results by Forrest and Mitchell [1993] on a problem with explicit hierarchically-defined building blocks showed a slight decrease in performance when introns were introduced.
A more thorough investigation of the benefits of introducing introns to GAs has been carried out by Wu and Lindsay [1995],Wu and Lindsay [1996a]. In [Wu and Lindsay, 1995], the authors confirm the findings of both Levenick [1991] and Forrest and Mitchell [1993]: demonstrating that the benefits of using introns does depend upon the fitness landscape of the problem being solved. Notably, the authors found that introns tended to increase the stability of existing building blocks within solutions whilst reducing the rate of discovery of new building blocks. This suggests that introns improve exploitation during evolutionary search but at the expense of exploration: behaviour which proved more effective upon versions of Forrest and Mitchell's functions with more levels (i.e. harder versions) and with larger fitness gaps between levels. In [Wu and Lindsay, 1996a], the authors extend their investigation to a fixed-length GA representation with `floating' building blocks, observing that performance improves - and soon surpasses the non-floating representation - as the proportion of introns increases. The authors suggest that this improvement is due to the role of introns in segregating building blocks and supporting linkage learning: a view which is also expressed by Harik [1997] and Lobo et al. [1997] in the context of linkage learning GAs (see section 7.5.1 for more information about these algorithms).
In genetic programming, almost all representations and representation languages have the potential to express code segments which have no (or very little) influence upon a program's outputs. These `introns' can be divided into two general classes20: syntactic and semantic. Syntactic introns are non-behavioural due to their context within a program, typically occurring below what Luke [2000] calls an `invalidator': structures such as OR(TRUE,X) and MULTIPLY(0,X) where the value of one argument has no influence upon the output of the function due to the value of another argument. Semantic introns, by comparison, are non-behavioural due to their content. Examples of semantic introns are NOT(NOT(...)) and ADD(SUBTRACT(...,1),1). Introns are sometimes also classified by whether or not they are executed [Angeline, 1998b]. For example, the syntactic intron X would be executed in the expression MULT(0,X) but would not be executed in the expression IF(FALSE,X). Semantic introns are always executed. Finally, it is possible for programs to contain effective introns: code segments which have very little effect upon a program. For example, in DIVIDE(X, RAISE(10,100)), most reasonable values of the effective intron X have a negligible effect upon the output.
In [Nordin and Banzhaf, 1995], the authors describe two roles of introns in GP: structural protection and global protection. Structural protection occurs when introns develop around a code segment, segregating it from other blocks of code and offering protection from crossover in much the same way as explicit introns in GAs. Global protection results from introns that offer neutral crossover sites and thereby discourage change to the program at a global level. Structural protection can only be offered by introns that exist at the interior of programs, since they must be placed around other code segments. This is only possible with semantic introns. Neutral crossover sites, however, can only occur below the program's functional code. Syntactic introns, which (in tree GP) are non-functional sub-trees, are therefore the principal source of global protection.
Nordin et al. [Nordin and Banzhaf, 1995,Nordin et al., 1996,Banzhaf et al., 1998] have investigated the benefits of introns in linear GP (see section 6.5.2 for an overview of linear GP). Both semantic and syntactic introns occur readily in linear GP. However, Nordin at al. wished to test whether the behaviour of the system could be improved through the use of explicit introns - which are easily introduced and varied by the system's genetic operators - and found that these, in concert with naturally occurring (implicit) introns, improved both the performance and generalisation abilities of the system. In tree-based GP, by comparison, it is widely believed [McPhee and Miller, 1995,Andre and Teller, 1996,Smith and Harries, 1998,Iba and Terao, 2000] that performance is almost always impeded by the presence of introns. For instance, McPhee and Miller [1995] maintain that introns are a major cause of bloat. Andre and Teller [1996] have shown that introns impair search by competing against functional code when size limits are in place. Smith and Harries [1998] found that explicit syntactic introns reduced the performance of GP, and Iba and Terao [2000] found, correspondingly, that removing syntactic introns improved performance.
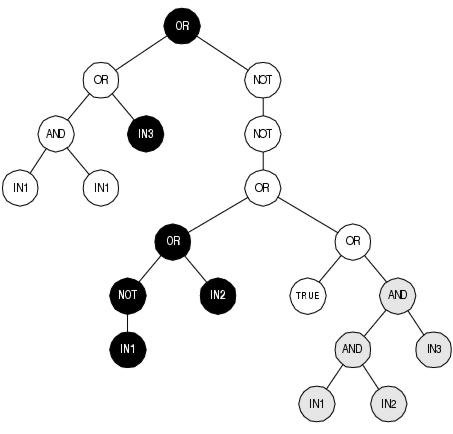
Figure 7.2: A GP expression tree containing introns. White nodes are semantic introns; grey nodes are syntactic introns. Expressed nodes, shown in black, represent the expression
OR(in3,OR(NOT(in1),in2)). Note how semantic introns can segregate coding areas.
Apparently, whilst introns are beneficial for linear GP (and GAs), they are detrimental for conventional tree-based GP (see figure 7.2 for an example of introns in a GP expression tree). Both Nordin et al. [1996] and Smith and Harries [1998] believe that this disparity lies within the different roles played by introns in the two different systems. In linear GP, introns convey benefit through their role in structural protection. In conventional GP, introns impair performance through their role in global protection. GP parse trees are recombined by swapping sub-trees. Syntactic introns, which are usually sub-trees, have a natural relationship with sub-tree crossover and are readily built, preserved and transmitted by this operator (a fact observed by Smith and Harries [1998] when trying to prevent the occurrence of introns). Semantic introns, by comparison, usually occur internally within sub-trees; and are more likely to be disrupted rather than constructed by sub-tree crossover. This means that within conventional GP there is a substantial bias towards construction and propagation of syntactic introns over semantic introns: and therefore a substantial bias towards global protection over structural protection. In effect, conventional GP suffers from too much global protection from crossover without gaining any benefits from structural protection. However, global protection can be reduced by limiting the growth of syntactic introns. Successful approaches include the removal of introns (the identification of which can be computationally expensive [Iba and Terao, 2000]) and limiting the behaviour of the crossover operator [e.g. Blickle and Thiele, 1994].
A redundant code is one for which there are more possible representations than there are entities to represent. Accordingly, some entities have more than one representation. Recently, a number of studies have investigated whether or not redundant codes can confer an evolutionary advantage over non-redundant codes in the context of genetic algorithms [Shipman, 1999,Shipman et al., 2000,Shackleton et al., 2000,Ebner et al., 2001,Knowles and Watson, 2002,Rothlauf and Goldberg, 2002,Barreau, 2002].
Work by Shipman et al. [Shipman, 1999,Shipman et al., 2000,Shackleton et al., 2000,Ebner et al., 2001], in particular, has looked at the role of neutrality during the evolution of entities represented by redundant codes. This work has made use of a variety of representations with differing levels of redundancy. These include a direct mapping, where each solution is represented by exactly one binary string; random mappings, where each solution is represented by many un-related binary strings; voting mappings, where binary solution traits are encoded by more than one bit in the binary string and where the trait is determined by voting between these bits; and more complex mappings where binary strings describe state machines whose operation determines the configuration of the solution. Apart from the direct mapping, all of these exhibit a high level of redundancy. However, analysis of the connectivity of their search spaces (where connections are determined by single point mutations) shows that these mappings differ considerably in their patterns of neutrality [Shackleton et al., 2000,Ebner et al., 2001]. Random mappings show very little neutrality, which is to be expected since there is no logical relationship between different encodings of the same solution. Where there is no epistasis (sharing of bits between building blocks), voting mappings exhibit no neutrality. Where there is epistasis, voting mappings exhibit large neutral networks with considerable connectivity between networks. However, some of the neutral networks are relatively isolated. Of the complex mappings, the random Boolean network (RBN) mapping (based upon Kauffman's model of gene expression) demonstrates the highest level of neutrality: exhibiting large neutral networks with very high connectivity between networks. In one configuration, 58% of mutations are neutral and each encoding has on average 21 non-neutral neighbours accessible through single point mutations.
In [Ebner et al., 2001], these mappings are applied to a number of optimisation problems: a random landscape search, a function with many local optima, and a dynamic fitness function. For all of these problems, performance on mutation-only search correlates with the connectivity of the mappings' neutral networks. The direct mapping is unable to solve the first two problems; in part due to insufficient maintenance of diversity. The non-epistatic voting representation exhibits behaviour which is almost identical to the direct mapping (an observation which is also made in [Rothlauf and Goldberg, 2002]). For the redundant mappings, diversity increases over time. These results have lead the authors to conclude that redundancy can be used to increase the performance of genetic algorithms: so long as the redundancy is organised in such a way that leads to neutral networks that percolate the search space.
However, Knowles and Watson [2002] were unable to reproduce these findings when they compared the performance of direct and RBN mappings upon a variety of more familiar EC problems. Indeed, aggregated across all the problems they tried, RBN mappings lead to worse solution times than direct mappings. Nevertheless, they did find that mappings with high neutrality showed far less sensitivity to mutation rate than non-redundant mappings. The authors speculate that the slower performance of RBN mappings may be due to the time overhead involved in random walks across neutral networks. Whilst these results do not support the conclusions of Ebner et al., they do not preclude the possibility that other redundant mappings might be more effective than the RBN mapping or that neutral networks might be important in solving larger or more rugged problems than GAs with non-redundant encodings are able to solve. Further criticism of the redundant mappings used by Shipman et al. can be found in [Rothlauf and Goldberg, 2002]: where the authors argue that complex mappings between representation and solution can lead to low locality; meaning that offspring will tend not to resemble their parents and evolution will tend to be ineffective. However, whilst the results presented in [Ebner et al., 2001] tend to refute this assertion, it does seem likely that the best use of redundancy can not be made through arbitrary mappings with no clear relationship between solution and representation.
| Symbol | Non-redundant | Redundant code | |
| A | 000 | 0 000 | 1 110 |
| B | 001 | 0 001 | 1 011 |
| C | 010 | 0 010 | 1 010 |
| D | 011 | 0 011 | 1 000 |
| E | 100 | 0 100 | 1 100 |
| F | 101 | 0 101 | 1 111 |
| G | 110 | 0 110 | 1 001 |
| H | 111 | 0 111 | 1 101 |
Table 7.1: An example redundant code of the type described in [Barreau, 2002] with one added redundant bit (left) which permutes the symbolic mapping of the coding bits when it is set. Notice the neutrality in the encoding of symbols C and E in the redundant code.
Barreau [2002] describes another approach to coding redundancy which introduces redundant coding bits that permute the existing encoding of a solution's building blocks. An example of this kind of redundant code is shown in table 7.1. The emphasis of Barreau's work lies in reducing the number of local optima which can be found during evolution: and thereby improving the adaptive performance of GAs. The best codes reduce the number of local optima by nearly a third on average across a range of symbolic mappings. Application of these codes to problems which have naturally non-redundant encodings shows that there is high correlation between a code's ability to remove local optima and its ability to improve evolutionary performance. On average, across three very different classes of problem, the best codes lead to an improvement in solution time of between two- and four-fold both with and without crossover. Interestingly, almost all redundant codings of this form reduce the presence of local optima (and therefore tend to improve performance) when their behaviour is averaged across a large number of problem instances. One group of codes in particular (whose mappings are based around rotation and symmetry) are guaranteed never to increase the number of local optima on any problem yet exhibit a marginal reduction in the number of local optima across all problems.
Barreau has also investigated the relationship between the neutrality found within his class of redundancy codes and their ability to reduce the number of local optima. However, the relationship is not linear; but rather there is a positive correlation up to a certain level (about 50% of maximum) after which increased neutrality tends to be associated with decreased reduction of local optima. The highest levels of neutrality are found in those codes which offer no or marginal reduction of local optima. Given the correlation between reduction of local optima and improvement in performance, these results would tend to support Knowles and Watson's view that too much redundancy can lead to reduced performance.
According to the terminology defined in [Rothlauf and Goldberg, 2002], the codes discussed above all exhibit more or less uniform redundancy: whereby every solution has roughly the same number of representations. However, it is also possible to define redundant codes in which certain solutions are over- or under-represented. This, according to Rothlauf and Goldberg [2002], leads to search biases which then reduce or increase performance depending upon whether optimal building blocks are over- or under-represented: and should therefore be taken into account when designing redundant codes or introducing redundancy to existing codes.
Functional redundancy occurs when a representation contains more functional information than is necessary to construct the entity that it represents. However, this extra functional information may still have significant evolutionary roles: for instance; (i) it may have been expressed in previous solutions and therefore represents a potential source of backtracking; (ii) it may be passed on to future solutions where it may become expressed; (iii) it is still subject to variation and may therefore evolve into new functionality; and more generally, (iv) it allows a population to maintain genetic diversity even when solutions have converged; and (v) it enables neutral evolution.
In many representations, sources of structural redundancy are also sources of functional redundancy. GP syntactic introns, for instance, consist of code. Whilst this code's meaning is currently irrelevant from a behavioural perspective, it still has a functional meaning and could be involved in any of the evolutionary roles outlined in the previous paragraph. Haynes [1996] has investigated the evolutionary advantage of functional redundancy in GP by constructing a problem in which each sub-tree's role is independent of its position within a parse tree. Sub-trees are not expressed in cases where they describe incomplete, invalid, duplicate or subsumed structures. Haynes found that removing these redundant sub-trees during evolution led to a reduction in performance (the opposite effect to that found by Iba and Terao [2000]): and attributed this to both loss of diversity and loss of protection from crossover. Haynes, however, was particularly interested in the impact of the loss of `protective backup' caused by the removal of duplicates of expressed structures; and therefore measured the change in performance caused by duplicating a solution's expressed sub-trees after all non-expressed sub-trees had been removed. Haynes found that more duplication of a solution's expressed sub-trees (duplicated up to seven times) led to faster solution times: suggesting that this kind of functional redundancy, at least, is beneficial to evolution. He also speculated that syntactic introns could be replaced by duplicated coding regions in non-positionally independent problem domains to achieve the same effect.
Angeline [1994] suggests that intronic structures like IF FALSE THEN X ELSE Y represent a form of emergent diploidy and dominance in GP: where sub-tree X corresponds to a recessive trait and sub-tree Y corresponds to a dominant trait. Changing the condition from FALSE to TRUE would then amount to a dominance shift. The concepts of diploidy and dominance have gained a lot of interest in the GA community [e.g. Smith and Goldberg, 1992,Dasgupta and McGregor, 1993,Collingwood et al., 1996,Levenick, 1999,Weicker and Weicker, 2001] as a way of handling non-stationary problems: problems where the search space changes over the course of time. Goldberg et al. [Goldberg, 1989,Smith and Goldberg, 1992] have developed a number of diploid representations for GAs. These use two chromosomes to encode each solution so that for each gene locus one chromosome contains a dominant allele and the other chromosome contains a recessive allele. Only the dominant allele is expressed in the solution. The most interesting of these is the triallelic scheme: where each allele has a value of either 1, 0, or 10; where 1 is dominant over 0 and 0 is dominant over 10. Mutation effectively has two roles under this scheme: it can change the value of an allele by changing a 1 into a 0 or vice versa, but it can also change the dominance of an allele by changing 1 into 10 or vice versa. In [Smith and Goldberg, 1992], the authors present results that show this diploid representation to be more effective than a haploid (single chromosome) representation upon a cyclic non-stationary problem: finding past optima both faster and with higher fidelity. In their own words: "diploidy embodies a form of temporal memory that is distributed across the population...this added diversity is more effective than that induced by mutation, because of its sensitivity to function history". Collingwood et al. [1996] have investigated the utility of higher levels of polyploidy in GAs for solving a range of test problems; finding that solutions with up to nine chromosomes can out-perform haploid representations.
Dasgupta's structured GA [Dasgupta and McGregor, 1992a,Dasgupta and McGregor, 1992b,Dasgupta and McGregor, 1993] uses a more complex dominance mechanism which uses analogues of regulatory genes to control the expression of other genes. The structured GA has a tree-like structure where genes at a higher level control groups of genes at lower levels. Genes at the lowest level, which may or may not be expressed depending upon the state of higher level genes, encode components of the solution. Dominance is enforced by limiting the number of regulatory genes which may be turned on at a given level. Dasgupta believes that the structured GA is more suitable for non-stationary functions than diploid GAs since whole blocks of genes may be turned on and off through a single regulatory gene mutation; and in [Dasgupta and McGregor, 1992b] presents results which show the structured GA achieving higher performance on the problem described in [Smith and Goldberg, 1992]. The structured GA also performs well on stationary problems. Results presented in [Dasgupta and McGregor, 1992a] show that the structured GA performs better than a conventional GA on a difficult engineering optimisation problem. Dasgupta believes that this is due to the structured GA's ability to retain greater genetic diversity.
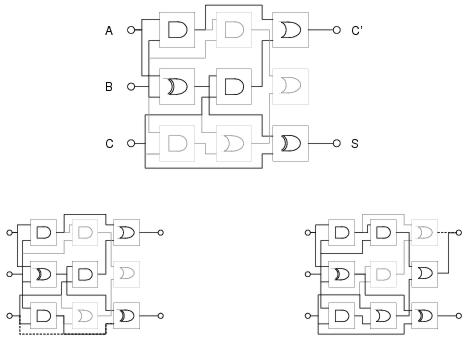
Figure 7.3: [top] A graphical example of a Cartesian GP circuit with functional redundancy. Components and connections shown in grey will not be expressed when the circuit is executed, [bottom left] but could become expressed if one of the expressed connections (shown in black) were to be re-routed following a mutation. [bottom right] A mutation could also result in behaviour akin to a dominance shift (see text).
In conventional GP, the level of functional redundancy is determined in part by the problem domain: since functional redundancy can only occur if the function and terminal sets can be used to construct introns. In cartesian GP, by comparison, functional redundancy occurs as a consequence of the way in which programs are represented: since the representation may define program components which are never referenced by coding components (see figure 7.3 for an example). This redundancy occurs irrespective of, and in addition to, redundancy allowed by the problem domain. Introns in both conventional and Cartesian GP have the potential to become expressed in descendant programs. In conventional GP, this is most likely to happen following a sub-tree exchange which moves a sub-tree from a non-coding position (syntactic intron) in one program into a coding position in another program. A non-coding sub-tree could also become expressed following a mutation which nullifies the invalidator of a syntactic intron: although in general this would only occur near the bottom of a program's parse tree and - especially in the later stages of search - would most likely be disruptive. In Cartesian GP, mutation plays a substantially different role since it is able to target the connectivity of program components in addition to their function. This means that mutation can cause un-expressed components to become expressed or expressed components to become un-expressed. It may also result in behaviours akin to dominance shift: with a dominant (expressed) sub-expression effectively being replaced by a recessive (un-expressed) sub-expression in the program. An example of this behaviour is shown in the bottom-right of figure 7.3.
Functional redundancy in Cartesian GP program representations provides an overt source of neutrality. From an evolutionary perspective, the components and interconnections defined in a Cartesian GP program's representation describe not just the currently expressed program but also capture the programs which can be accessed through single changes to the input connections of expressed components. Changing the functions and inter-connections of functionally redundant components does not change the program that is currently expressed, but does change the programs that are available through single point mutations. In [Vassilev and Miller, 2000], the authors find that when these neutral mutations are not allowed, the best fitness attained when evolving three-bit multiplier circuits is significantly lower than that achieved when neutral mutations are allowed. Furthermore, results reported in [Yu and Milller, 2001] and [Yu and Miller, 2002] suggest that even large neutral changes (equivalent to hundreds of point mutations) play a significant role in improving search performance.
A related view of the kind of functional redundancy seen in Cartesian GP is that it provides a form of multiplicity: where, in a sense, a program's representation describes more than one potential program (this view of functional redundancy is discussed in Harik [1997] and Lones and Tyrrell [2001b] in the context of other EAs). Given that the components in the representation have common ancestory, it seems likely that these potential programs would have related functionality. This idea is taken further by Oltean and Dumitrescu [2002]; who describe a GP system - multiple expression programming - that resembles Cartesian GP but which measures a program representation's fitness according to all the programs that it could potentially express through single changes to the input connections of the output nodes. In effect, fitness captures the level of adaptation in the local neighbourhood of the search space. The authors report good performance across a range of standard GP problems: suggesting that there is a benefit to this approach; although there is inevitably a performance overhead. Presumably there is also the potential for search being disrupted in more rugged landscapes: where the variance of the fitness of the individual programs described by a program representation may be high. A recent paper by Hornby, [2003] introduces another approach to encoding multiple solutions within a single representation, using it to evolve parameterised design families.
It is perhaps taken for granted by biologists; but from the perspective of evolutionary computation, independence between the behaviour of a gene product and the position of its gene locus is a significant source of de-constraint within biological representations. Within most EC representations the meaning of a genetic component is determined by its absolute or relative position. This inevitably leads to problems during recombination. In GAs it may not be possible to find an optimal solution if components of optimal building blocks are assigned positions that are too far apart in the solution chromosome. In most forms of GP a component's context is determined by its position within the program representation. Given that crossover does not typically preserve a component's position, it is quite likely that its context, and therefore its function, will be lost following recombination. This section discusses existing approaches to removing positional dependence from EAs.
Linkage learning is the GA analogue of epistatic clustering. Linkage learning is motivated by the desire that all the genetic members of a building block should be inherited together during recombination in order to prevent their destruction. According to Smith [2002]: "for a problem composed of a number of separable components, the genes in the building blocks coding for the component solutions will ideally exhibit high intra-block linkage but low inter-block linkage [to encourage exploration]". The simplest approach to linkage learning involves limiting crossover so that it is less likely or unable to fall between genes whose alleles are considered to belong to the same building block. This is typically achieved by using crossover templates (successful approaches include those by Rosenberg [1967] and Schaffer and Morishima [1987]), though it may also be encouraged with explicit introns (see section 7.4.1). However, these approaches do not target the underlying cause of the linkage problem: positional dependence. Rather, they cause a kind of implicit epistatic clustering which is unlikely to benefit linked genes located far apart in the solution chromosome. Such a situation can only be remedied by moving the genes closer together within the chromosome. However, for most problems the optimal ordering of genes is not known in advance. Furthermore, it is generally not desirable for a genetic algorithm to rely upon domain knowledge.
An obvious solution to this problem is to allow the ordering of genes within a chromosome to evolve. This requires that a gene can occupy any position within the chromosome without losing its original context. Typically this is achieved by associating each gene allele with some kind of identifier which - in the absence of positional information - shows the gene locus that it corresponds to. A prominent early example of this approach is Bagley's inversion operator. However early approaches such as Bagley's had little success, primarily due to competition between selection for fit solutions and selection for fit orderings; not to mention the problem of designing crossover operators which can appropriately recombine solution chromosomes with different orderings and the associated problems of under- and over- specification of gene alleles. Nevertheless, these so-called `floating representation' approaches have proven successful in domains where under- and over- specification is not an issue [Raich and Ghaboussi, 1997,Wu and Lindsay, 1996a].
The messy GA [Goldberg et al., 1993] was the first broadly successful approach to use a floating representation to achieve linkage learning. The messy GA is an iterative algorithm where each iteration consists of a primordial phase: where building block identification takes place; and a juxtapositional phase: where building blocks are assembled into complete solutions. During each iteration, the algorithm attempts to identify and assemble higher level building blocks. Candidate solutions are represented by variable length chromosomes consisting of < locus,allele > pairs. Each gene locus may be associated with any number of alleles. Where a locus is associated with more than one allele, the one which is defined nearest the left of the chromosome will be used during the solution's evaluation. If a solution has no alleles defined for some of its gene loci, values are taken from a template chromosome. The best solution found within the juxtapositional phase of a particular iteration is used as the template chromosome for the next iteration. The template chromosome for the first iteration is randomly generated. The aim of the algorithm is for the template chromosome to contain optimal building blocks up to the current level and form the basis for the discovery of higher level building blocks in subsequent iterations.
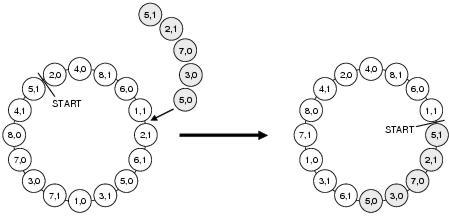
Figure 7.4: Recombination in Harik's Linkage Learning GA.
The messy GA offers superior performance to simple GAs on problems with high levels of epistasis; and it does this by overcoming the problems which limited the applicability of earlier linkage learning approaches. Significantly, by separating building block identification from the assembly of building blocks to form solutions, the messy GA avoids competition between finding fit solutions and fit orderings. However, the algorithm is complex to implement and sensitive to parameter values, making it difficult to tune for a given problem domain. For these reasons, Harik [1997] proposed a linkage learning GA (the LLGA) based upon a conventional GA framework but with a representation and crossover operator derived in part from the messy GA. The LLGA, like the messy GA, uses chromosomes consisting of < locus,allele > pairs. Unlike the messy GA, these chromosomes are circular and contain one copy of every allele of every gene locus. Both the position at which interpretation starts and the ordering of the alleles determines how the chromosome is interpreted. Different starting locations can lead to a chromosome being interpreted in different ways. Crossover takes the form of copying a contiguous sequence of < locus,allele > pairs from a donor chromosome and then grafting it into a recipient chromosome, removing existing copies of the newly grafted < locus,allele > pairs from the recipient chromosome (see figure 7.4 for an example). The effect of crossover is to re-arrange the ordering of both alleles and gene loci within a chromosome: changing both its interpretation and the linkage between its gene loci. Whilst unlike the messy GA the LLGA does not separate building block identification from building block assembly, it does avoid the problems with crossover and under- and over-specification found with earlier approaches and does avoid the complexities of the messy GA.
Floating representation has also been used within GP; though with limited success. In a biologically-inspired system described by Luke et al. [1999], a finite state automata is represented by a sequence of `genes'; each of which is identified by a pattern, describes a state, and declares its connections in terms of the identity patterns of other genes. During a development process, each state attempts to connect to states whose patterns most closely match its input patterns. Whilst able to solve a range of string classification problems, this method shows little improvement over conventional GP.
An altogether different approach to positional independence can be seen in Wu and Garibay's proportional GA and Ryan et al's Chorus GP system; where both sets of authors have taken inspiration from the role of protein concentration within gene expression. The proportional GA uses variable-length chromosomes comprised of symbols taken from a parameter alphabet; where each symbol corresponds to a particular parameter. The value of a parameter is determined by the proportion of its corresponding symbol within a chromosome - in much the same way that certain phenotypic traits are determined by the concentration, rather than just the presence, of a particular gene product. The precision with which each parameter is described depends upon the length of the chromosome: a factor which, the authors believe, leads to competition between solution length and precision. Across a range of problems, the proportional GA offers at least as good performance as the simple GA; with significantly better performance upon certain problems. The authors attribute this improvement to the proportional GA's ability to reduce the size of the search space by sacrificing unnecessary precision.
Ryan et al's Chorus system is based upon grammatical evolution. In GE, the meaning of a gene is calculated respective to the current grammar transition. In Chorus, by comparison, each gene refers to a specific rule within the grammar. As for GE, a Chorus program is interpreted from left to right. However, a gene only causes a grammar rule to be fired if it refers to a transition which is currently applicable: and only if there are no other relevant rules waiting to be expressed. If a gene refers to a rule which cannot currently be applied, the rule's entry in a `concentration table' is incremented; showing that it is waiting to be expressed. Accordingly, a particular gene might have either an immediate or a delayed effect; meaning that its position within the program is not necessarily indicative of when it will be executed. However, possibly due to the greater fragility of its representation towards the effects of mutation, Chorus programs appear not to evolve as well as GE programs [Azad and Ryan, 2003].
This chapter has introduced four different approaches to improving the evolvability of the artefacts which are evolved by evolutionary computation techniques: homologous recombination, pleiotropy, redundancy, and positional independence. Whilst this review is biased towards techniques which adapt representation rather than those which adapt variation, it is interesting to note that homologous crossover can lead to an improvement in evolutionary performance. However, this performance gain is only significant for linear GP: which has a representation which easily supports homologous recombination. For conventional tree-based GP, the difficulty of implementing homologous recombination is reflected by a high computational overhead and little improvement in performance. By comparison, the introduction of pleiotropy (genetic re-use) into tree-based genetic programming has proved a very successful approach. This tends to reflect the biological viewpoint that a degree of pleiotropy helps evolution by preventing the need to re-evolve identical sub-structures more than once. The tendency for evolving programs to make use of implicit re-use within graph-based representations also supports this point of view.
Redundancy plays a range of interesting roles in evolutionary computation. Its capacity to provide structural protection from change has been the subject of a number of investigations. There appears to be some benefit to introducing structural redundancy into GA representations, particularly floating representations. Tree-based GP exhibits a high level of natural structural redundancy. However, this redundancy is generated by syntactic introns which accumulate at the bottom of programs; providing global protection to change which degrades performance and causes bloat. Nevertheless, results from linear GP suggest that appropriate forms of non-coding components can lead to better performance and better solution generality: though unfortunately this kind of redundancy is inherently unstable within tree-based GP.
Research into coding redundancy in GAs also suggests that performance gains should only be expected when redundancy is suitably organised. For example, codes which use redundancy to remove local optima generate a proportional increase in performance. However, there is some debate over the utility of neutrality within codes; though it appears that a degree of neutrality can benefit search by maintaining higher diversity within a population; although too much neutrality appears to reduce performance, possibly by reducing solution locality and introducing extra search overheads.
The functional role of redundancy is particularly interesting, though perhaps least understood. Functional redundancy plays a particularly important role when solving non-stationary problems, where it helps to buffer previous solutions. However, it is also known to improve performance upon stationary problems in both GA and GP: though again the organisation of redundancy appears to be an important determining factor. The value of functional redundancy is perhaps best seen within approaches like multiple expression programming which make explicit use of non-coding components in evaluating a solution.
From the perspective of evolutionary computation, positional independence in biology seems like an important source of evolvability. Linkage learning GAs show how positional independence can be successfully introduced into EC representations. Positional independence can also be introduced to GP, but so far only within non-tree based systems and without any significant increase in performance.
On the whole, the research reviewed in this chapter supports the notion that biological concepts can be used within evolutionary computation in order to improve evolvability. What is perhaps less clear is that this research also impacts upon our understanding of biology, where current understanding of evolvability is mostly at a theoretical rather than experimental level. For instance, pleiotropy is evidently a powerful source of evolvability within EC: and this supports the idea that pleiotropy is also important within biological evolution - and future EC research could give more insight into what is an appropriate balance between pleiotropy and compartmentalisation. EC research also supports biological theories of the role of non-coding DNA in affirming structural protection. However, in other regards biological theories of redundancy are more advanced than EC practice. The role of redundancy structures in supporting gradual molecular evolution, for instance, could be an interesting inspiration for future EC research. Furthermore, future research directions could be measured more by the topics which are not covered in this chapter rather than those that are. For example: multiple weak interactions, exploratory mechanisms, epigenetic inheritance, and ecological interactions are all thought important in the evolution of biological systems.
20Note that this terminology is not standard and conflicts with taxonomies offered by other authors.