|
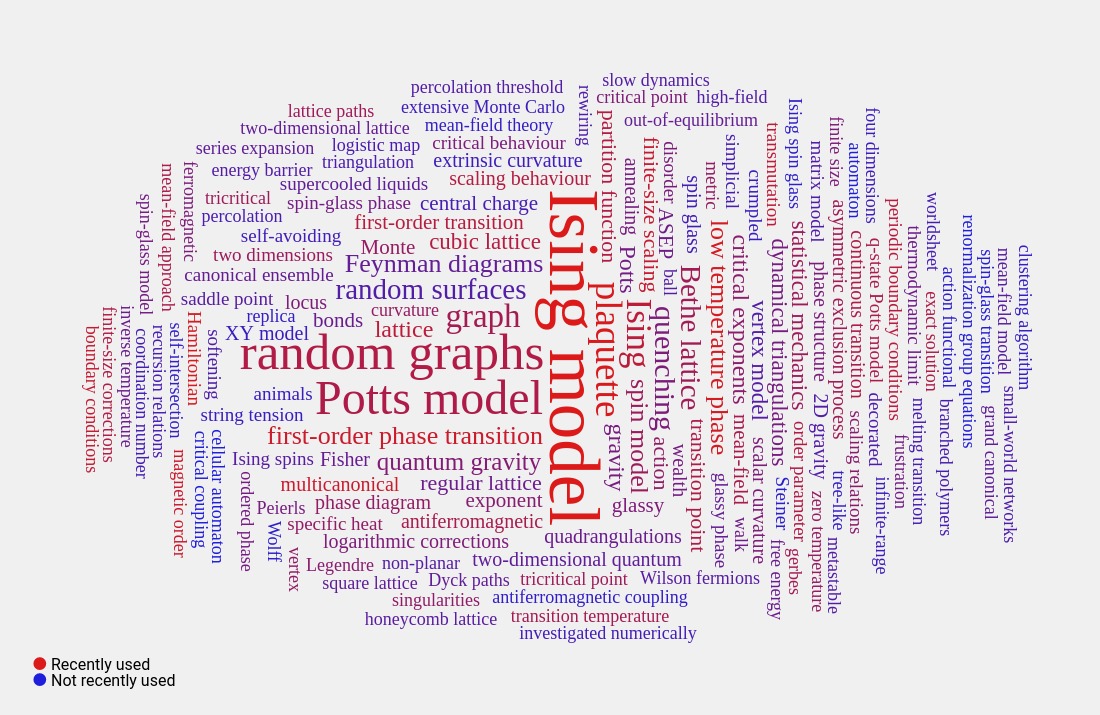
(Fairly) Current Research Interests: 3D Plaquette Ising Model, Fractons etc
I keep circling back to the 3D Plaquette Ising Model, having first run across it many moons ago when we discovered that it had a first order phase transition (which was bad news at the time, since we were looking for continuum limits).
Much more recently work with Marco Mueller and Wolfhard Janke of Leipzig University found non-standard scaling behaviour at the first order transition since the the low temperature phase is highly degenerate as the result of a subsystem symmetry, intermediate between a global and a local (gauge) symmetry.
Such subsystem symmetries have recently been implicated in fractonic models, in which quasiparticle excitations display restricted (or even zero) mobility.
Indeed, gauging the subsystem symmetry in the quantum 3D Plaquette Ising Model gives rise to a canonical fractonic model, the X-cube model, in much the same way as gauging the global symmetry of the standard quantum 2D Ising model gives rise to the toric code.
|
(Fairly) Recent Papers
- D. A. Johnston and Ranasinghe P.K.C.M. Ranasinghe, (Four) Dual Plaquette 3D Ising Models, Entropy 22(6), 633 (2020)
- D. A. Johnston, Lattice SUSY for the DiSSEP at λ2 = 1 (and λ2 = −3), J. Phys. Commun. 3 105011 (2019)
- D. A. Johnston, M. Mueller and W. Janke, Plaquette Ising models, degeneracy and scaling, Eur. Phys. J. Special Topics,
226, Issue 4, 749–764 (2017)
- M. Mueller, W. Janke and D. A. Johnston, Exact solutions to plaquette Ising models with free and periodic boundaries, Nucl. Phys. B 914, 388-404 (2017)
- M. Mueller, W. Janke and D. A. Johnston, Macroscopic Degeneracy and Order in the 3d Plaquette Ising Model, MPLB Vol. 29 1550109 (2015)
- M. Mueller, W. Janke and D. A. Johnston, Planar ordering in the plaquette-only gonihedric Ising model, Nucl. Phys. B894, 1-14 (2015), [arxiv:1412.4426]
- M. Mueller, W. Janke and D. A. Johnston, Transmuted Finite-Size Scaling at First Order Phase Transitions, Physics Procedia Vol. 57, 68-72 (2014), [arxiv:1410.7928]
- D. A. Johnston, ℤ2 lattice gerbe theory,
Phys. Rev. D 90, 107701 (2014), [arXiv:1405.7890]
- M. Mueller, W. Janke and D. A. Johnston, Multicanonical analysis of the plaquette-only gonihedric Ising model and its dual, Nucl. Phys. B888, 214-235 (2014), [arXiv:1407.7252]
- M. Mueller, W. Janke and D. A. Johnston, Nonstandard Finite-Size Scaling at First Order Phase Transitions, Phys. Rev. Lett. 112, 200601 (2014), [arxiv 1312.5984]
Coauthors from Heriot-Watt PURE
|